Введение. Биофизика – это наука, возникшая на стыке двух фундаментальных наук – биологии и физики

Биофизика – это наука, возникшая на стыке двух фундаментальных наук – биологии и физики. В биофизике роли этих наук распределяются следующим образом: биология предоставляет объект исследования, а физика – метод. Задачей теоретической биофизики является установление механизмов функционирования биосистем, опираясь на фундаментальные физические законы и используя аппарат и методы анализа теоретической физики. Объектом теоретического исследования современной молекулярной биофизики являются макромолекулярные биологические системы, для которых установлена их микроскопическая структура (рентгеноструктурный анализ) и выявлена их биологическая функция. Теоретический анализ предполагает установление элементарных механизмов и условий их реализации в обеспечении функционирования данных молекулярных биосистем. Под элементарными механизмами, обусловливающими выполнение биосистемой заданной функции, понимаются молекулярные процессы, протекающие под действием сил межатомных и межмолекулярных взаимодействий. Теоретическое рассмотрение этих взаимодействий возможно только в рамках квантовой механики. Конкретные задачи, которые необходимо при этом решать, являются весьма сложными и трудоемкими. На современном этапе подобные задачи решаются численными методами с помощью компьютерного моделирования. Вместе с тем, некоторые существенные детали общих молекулярных механизмов можно понять, основываясь на рассмотрении упрощенных моделей. От читателя при этом потребуется наличие только самых элементарных квантовых представлений, а также некоторых сведений из общего курса физики. Надеемся, что после проработки данного раздела у читателя возникнут как понимание, так и необходимые навыки для самостоятельного анализа подобных задач.

Некоторые способы «правдоподобных рассуждений»

В качестве иллюстрации методологии, используемой в этом разделе, приведем пример [1], с помощью которого можно понять общий подход в проведении качественных квантовомеханических рассуждений, а также убедиться в реальности числовых оценок, получаемых с помощью простых моделей. Всем еще из школьного курса химии известны соединения с так называемыми сопряженными связями, т.е. когда происходит чередование одинарных и двойных связей. Классическим примером соединения с сопряженными связями является молекула бензола C₆H₆. Такие соединения обладают особыми электронными свойствами – π-электроны обобществлены (делокализованы) в сопряженных цепях и могут перемещаться вдоль цепи почти свободно, подобно тому, как это происходит в металлах. Если, например, молекулу бензола поместить во внешнее магнитное поле, то в молекуле возникнет круговой ток, который создаст магнитный момент молекулы, направленный против внешнего поля (диамагнетизм).

Рассмотрим линейную цепочку с сопряженными связями, например, такую

H₂C==CH—CH==CH—CH==….—CH==CH₂,

в которой группа C==C—C является элементарным звеном цепи длиной l. Если цепь имеет N таких звеньев, то длина всей цепочки будет L = N l. Каждая такая групп содержит два π-электрона, следовательно, общее число π-электронов в цепи равно 2N. Эти электроны могут почти свободно перемещаться вдоль цепи, но не могут покинуть молекулу (потенциал ионизации таких молекул достаточно высок, порядка 10 эВ [2]). Основываясь на этом, мы можем представить, что π-электроны данной молекулярной цепочки заключены в прямоугольном потенциальном ящике с бесконечно высокими стенками (рис. 3.1). Пусть электроны в ящике движутся со скоростями v, тогда им соответствует дебройлевская волна длиной 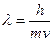, где h – постоянная Планка, m – масса электрона. В силу допущения о бесконечно высоких стенках потенциального ящика эти волны не могут выйти за его пределы, и на границах ящика амплитуда этих волн обращается в ноль. Поэтому в ящике образуются стоячие волны с узлами на границах ящика. Эта ситуация аналогична классической задаче о колебаниях струны, закрепленной на концах. В такой струне можно возбудить стоячие волны, длины λ_n которых связаны с длиной L всей струны условием 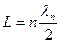, т.е. на длине струны должно укладываться целое число n полуволн. Из соотношения ДеБройля получим выражение для скорости электрона 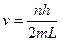. Внутри ящика электроны обладают только кинетической энергией 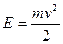, т.к. потенциальная энергия равна нулю. Подставив сюда выражение для скорости, получим энергетический спектр электронов в ящике

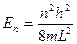. (3.0)

Таким образом, мы определили π-электронные энергетические уровни в молекулярной цепочке с сопряженными связями.Согласно принципу запрета Паули для частиц с полуцелым спином, на каждом уровне может располагаться не более двух электронов с антипараллельными спинами (рис. 3.1). Всего тогда будет занято N энергетических уровней.

Оценим теперь частоту поглощения наиболее длинноволновой части спектральной полосы ω = (E_N+1 – E_N)/ħ. Заметим, что в формулах одинаково часто встречаются постоянная Планка h и перечеркнутая постоянная Планка ħ. Они связаны друг с другом простым соотношением 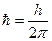и используются из соображений удобства написания формул, аналогично тому, как используются линейные и циклические частоты 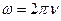. Подставив в формулу выражения для энергий и используя определение для L, получим выражение для частоты поглощения

.

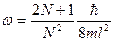Рис. 3.1. Модельный потенциал для π-электронов молекулярной цепочки с сопряженными связями. Показаны энергетические уровни, на каждом из которых находится по два электрона с противоположными спинами. Переход электрона с верхнего занятого уровня N на нижний свободный уровень N+1 сопровождается поглощением кванта электромагнитной волны частотой ω.

Если N >> 1, то единицей в числителе можно пренебречь по сравнению с 2N и для длины волны поглощения получим выражение

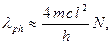
где с – скорость света. Если принять длину звена l ≈ 2 Ǻ, то из этой формулы получим

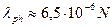см

Из этой формулы следует, что с удлинением молекулярной цепи с сопряженными связями ее полоса поглощения сдвигается в длинноволновую область, что находит подтверждение в эксперименте. Цепи, содержащие шесть и более звеньев, поглощают в видимой области спектра, т.е. являются окрашенными. Так, например, при N = 8 для длины волны получим оценку 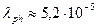см, что соответствует желто – зеленой части спектра видимого излучения. Известно, что органические красители – это всегда молекулярные системы с сопряженными связями.

Из приведенного примера можно сделать, по крайней мере, два вывода. Во-первых, для получения качественных результатов не всегда надо решать уравнение Шредингера для исследуемой квантовой системы. Можно использовать аналогию с волновыми процессами. Во-вторых, имеет смысл первоначально максимально упростить исходную систему, сохранив в ней только некоторые существенные черты. Если получаемые при этом качественные результаты согласуются по порядку величины с известными данными, то это означает, что модель правильно отражает особенности системы. Дальнейшее усложнение модели должно, по идее, привести к улучшению количественного согласия с экспериментом, но принципиальных изменений, если, конечно, в модель не привносится что–либо принципиально новое, не должно наблюдаться.

Для того, чтобы овладеть искусством качественных рассуждений необходима определенная база математического и физического образования. На пустом месте ничего не родится. Физическая интуиция, к которой часто апеллируют при качественных рассуждениях, является, на самом деле, результатом достаточно большого опыта. Студентам – биофизикам, пришедшим в эту науку из биологии, подчас достаточно трудно увидеть «за деревьями лес», т.к. их физико-математическое образование порой не «дотягивает» до необходимого уровня. Приведем в этой связи такой пример. При обсуждении квазиклассического приближения, которое широко используется в биофизике, получают следующее условие его применимости |dλ/dx| << 1, где λ – дебройлевская длина волны частицы, движущейся в заданном потенциале U(x). Зададим вопрос, как можно оценить эту производную и, соответственно, почувствовать физический смысл этого условия? Попытайтесь ответить на этот вопрос. Рассуждения могут быть примерно такими. Из курса математического анализа известно, что по своему физическому смыслу производная функции характеризует скорость ее изменения в заданной области определения. Если эта производная мала, то, следовательно, функция мало меняется, когда аргумент пробегает заданный интервал значений. Что это может означать с физической точки зрения? Примерно следующее. Если область пространства, в которой движется частица, имеет линейные размеры порядка l, то производную можно приближенно оценить таким образом dλ/dx ~ λ/l. Отсюда следует, что условием квазиклассического приближения является условие малости дебройлевской длины волны по сравнению с линейными размерами области, в которой движется частица, λ << l. В качестве полезного упражнения мы предлагаем читателю обосновать справедливость данной оценки производной. Для этого надо учесть, что потенциал U(x), в котором движется частица, является плавной функцией координат. Для лиц, желающих подробнее разобраться в методах подобных приближенных оценок, мы рекомендуем книгу [3].