Раздел 2. ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ ПРОЦЕССОВ

О.Г. Лунева, А.А. Черкашин, А.О. Шумарина, П.А. Мамонов

Основные понятия и законы термодинамики

Предметом термодинамики является изучение закономерностей тепловой формы движения материи и связанных с ней физических явлений. Термодинамика изучает закономерности теплового движения в равновесных системах и при переходе систем в равновесие (равновесная термодинамика), а также обобщает эти закономерности на неравновесные системы (неравновесная термодинамика, или термодинамика необратимых процессов). Термодинамической системой может являться любой макроскопический материальный объект. Выделение термодинамической системы состоит в указании границы, отделяющей ее от остального, внешнего по отношению к данной системе, мира.

В зависимости от характера обмена энергии и массы с окружающей средой через границы системы различают три группы систем:

- изолированные – не обмениваются с внешней средой ни энергией, ни массой,

- закрытые – обмениваются с внешней средой энергией, но не могут обмениваться массой,

- открытые – обмениваются с внешней средой массой и энергией.

Процессы, протекающие в системе, бывают:

- обратимыми (равновесными) – протекают в системе таким образом, что вызванные ими изменения в состоянии системы могут произойти в обратной последовательности без дополнительных изменений в окружающей среде,

- необратимыми (неравновесными) – протекание этих процессов в обратном направлении сопровождается остаточными изменениями в окружающей среде.

В равновесном состоянии системы свойства системы не изменяются во времени и в ней отсутствуют направленные потоки вещества и энергии.

В неравновесном состоянии системы малые воздействия могут вызвать изменение состояния системы.

В стационарном состоянии системы свойства системы не изменяются во времени, но присутствуют направленные потоки вещества и энергии, взаимно уравновешивающие друг друга.

Пусть в системе протекают последовательные химические реакции

,

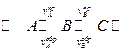Тогда скорость изменения концентрации вещества В

,

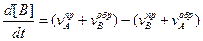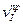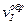где и - скорости прямой и обратной реакций, соответственно.

В равновесном состоянии

;

.

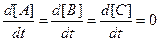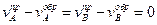В стационарном состоянии

.

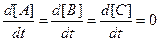
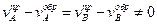В неравновесном состоянии

.

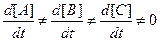Первый закон термодинамики – это закон сохранения энергии в применении к процессам преобразования теплоты. Его математическая формулировка:

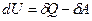, (2.1)

где 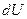- изменение внутренней энергии системы, 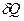- количество переданной системе теплоты, 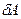- работа.

В системе, где протекает химическая реакция, 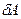включает работу против сил внешнего давления 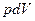и максимально полезную работу 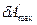, сопровождающую химические реакции

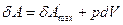. (2.2)

Знаки теплоты и работы выбирают следующим образом: теплота считается положительной, если она передается системе; работа считается положительной, если она совершается системой над окружающей средой.

При постоянном давлении вводится еще одна функция состояния системы – энтальпия Н

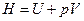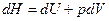, . (2.3)

Как правило, химические реакции протекают при постоянных давлении и объеме. В этих условиях теплота является функцией состояния.

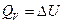при постоянном объеме,

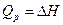при постоянном давлении.

Величины 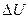и 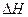зависят только от начального и конечного состояния системы и не зависят от пути, по которому может происходить превращение. Большинство биохимических процессов протекает при постоянном давлении, а объем системы почти не меняется, тогда .

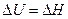Зная теплоты образования продуктов реакции и реагентов, можно вычислить выделившуюся или поглощенную теплоту химической реакции, так как тепловой эффект реакции, протекающей при постоянном давлении и объеме, не зависит от пути реакции, а определяется только разницей энтальпий исходных веществ и продуктов реакции (закон Гесса):

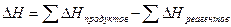. (2.4)

Это соотношение позволяет вычислить 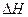для любой химической реакции, в том числе для реакций, которые невозможно изучать экспериментально.

Изменение энтальпии при образовании 1 моль химического соединения из простых веществ, находящихся в наиболее устойчивом стандартном состоянии (1 атм, 25˚С) называется стандартной теплотой образования данного вещества (ΔН^°). Энтальпия образования устойчивых простых веществ в стандартном состоянии принимается равной нулю при любой температуре.

Если ΔН^° - отрицательная величина, то тепло выделяется в результате реакции. Теплота образования характеризует прочность химических связей, образовавшихся в результате реакции, то есть - ΔН^° выражает количество тепла, которое надо «ввести» в соединение, чтобы разорвать его связи и образовать индивидуальные элементы. Для определения энтальпии образования конкретной химической связи надо обратиться к более простой молекуле. Например, биоорганические молекулы имеют связь С−Н и для того, чтобы определить ΔН^° этой связи, можно рассмотреть образование молекулы метана СН₄ из простых веществ.

При нагревании системы температура увеличивается пропорционально количеству поглощенного тепла, коэффициентом пропорциональности является теплоемкость

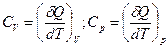, (2.5)

где символы V и р обозначают процесс, проходящий при постоянном объеме и давлении.

Средняя теплоемкость для одного моля вещества определяется выражением

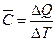. (2.6)

Для идеального газа теплоемкость можно выразить и через изменение внутренней энергии. При постоянном объеме механическая работа не совершается и теплота равна изменению внутренней энергии, поэтому

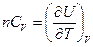, (2.7)

где n –количество молей идеального газа. При постоянном давлении

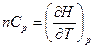. (2.8)

Второй закон термодинамики позволяет определять возможность и направление протекания термодинамических процессов. Он утверждает, что протекающий в изолированной системе самопроизвольный неравновесный процесс всегда вызывает увеличение энтропии до ее максимальных значений при окончании процесса и установлении термодинамического равновесия.

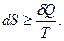(2.9)

Для системы, не совершающей теплообмена с внешней средой, 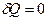и уравнение принимает вид

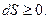(2.10)

Следовательно, в изолированной системе энтропия остается неизменной в равновесных и возрастает в неравновесных процессах.

В отличие от первого закона термодинамики, имеющего абсолютное значение, второй закон носит статистический характер, т.е. увеличение энтропии в необратимых процессах отражает лишь наиболее вероятное их направление. Этот закон соблюдается наиболее точно для макроскопических систем с большим количеством молекул, где вероятности отклонения от среднестатистического их распределения в объеме системы крайне малы. В системах с малым количеством частиц вероятность таких отклонений увеличивается. Число возможных микросостояний, или способов распределения частиц, которыми осуществляется данное макросостояние системы, называется термодинамической вероятностью. Больцман установил связь между энтропией системы S и термодинамической вероятностью ее состояний W

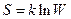. (2.11)

Термодинамические потенциалы (характеристические функции) – это термодинамические функции, которые выражают в явном виде все термодинамические свойства системы. Термодинамическими являются функции U – внутренняя энергия, H – энтальпия, F= U-TS - свободная энергия Гельмгольца (изохорно-изотермический потенциал), G=H-TS – свободная энергия Гиббса (изобарно-изотермический потенциал). Потенциальная функция, будучи продифференцирована по перемещению, дает силу, стремящуюся перевести или возвратить систему в равновесие.

На основании первого и второго законов термодинамики для равновесных (обратимых) процессов термодинамические потенциалы связаны следующими уравнениями:

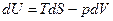, (2.12)

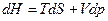, (2.13)

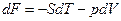, (2.14)

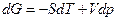. (2.15)

Эти уравнения справедливы для закрытых систем, где совершается только механическая работа. В термодинамических расчетах удобно применять последние два потенциала, так как их естественные переменные удобны для систем, где протекают химические реакции.

Изменение любого вида энергии, сопровождающее изменение количества вещества в системе называется химическим потенциалом µ, то есть

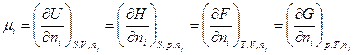, (2.16)

где n_i – число молей i-го компонента системы, n_j – постоянные количества всех компонентов кроме i-го.

Так как химические реакции, как правило, протекают при постоянных температуре и давлении, целесообразно использовать свободную энергию Гиббса, так как в этих условиях она обладает свойствами потенциала. Если происходят химические реакции или система является открытой, тогда

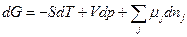, (2.17)

где µ - химический потенциал, - количества веществ.

Если в системе имеет место изменение заряда системы, вместо химического потенциала используется электрохимический потенциал:

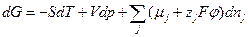, (2.18)

где 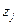- заряд, F – число Фарадея, φ – электрический потенциал.

Уменьшение энергии Гиббса в случае обратимого процесса при постоянстве температуры и давления равно максимально полезной работе, которую может совершить система:

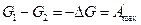. (2.19)

При неравновесных процессах 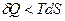и работа будет меньше, чем максимальная работа равновесного процесса, тогда в общем виде для равновесных и неравновесных процессов:

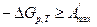. (2.20)

Пример 2.1. Вычислить стандартную теплоту образования угарного газа, если известно, что для реакции

С+О₂→СО₂ 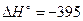кДж/моль СО₂,

а для реакции

2СО+О₂→2СО₂ 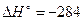кДж/моль СО₂.

Решение: Данные химические реакции можно представить, как показано на рис. 2.1.

Рис. 2.1.

Тогда для химической реакции 2С+О₂→2СО

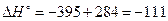кДж/моль СО.

Химическую реакцию образования угарного газа из простых веществ невозможно провести экспериментально, так как часть углерода сгорает с образованием углекислого газа, поэтому энтальпию этой реакции можно только вычислить.

Пример 2.2. Вывести формулу для изменения энтропии ΔS одного моля идеального газа при изобарном нагревании (T₀ – начальная температура, Т – конечная температура).

Решение: Согласно выражению (2.12)

.

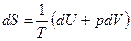Из уравнения (2.7) и 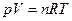(уравнение состояния идеального газа):

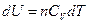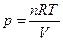, , тогда

.

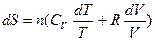После интегрирования .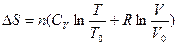

При р=const 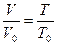, тогда .

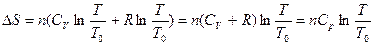Для 1 моль идеального газа .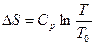

Пример 2.3. Получить выражение для химического потенциала одного моля идеального газа при постоянном давлении и температуре.

Решение: Химический потенциал при постоянном давлении это молярная энергия Гиббса (2.16).

Для 1 моль идеального газа .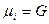

Из выражения (2.15) при постоянной температуре получаем

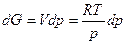
Интегрируем от G₀ до G и от р₀ до р:

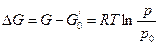
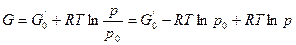
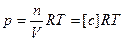, тогда

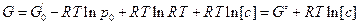
Т.к. для 1 моль идеального газа 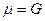, то

.

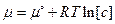Пример 2.4. Температура плавления α-спирали составляет 50˚С. Энтальпия перехода спираль-клубок — 113 кДж·моль^-1. Определить: а) энтропию перехода спираль-клубок; б) длину спирали, принимая, что выход каждого остатка из спирали добавляет системе по 3 степени свободы, и соответствующие координаты имеют по два устойчивых положения (система устойчива при двух значениях соответствующих координат); в) энтальпию разрыва водородной связи спирали.

Решение: а) Плавление спирали соответствует ситуации когда свободная энергия перехода спираль — клубок становится равной нулю:

.

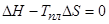Отсюда,

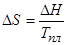
Энтропия перехода равна 350 Дж·моль^-1·К^-1.

б) Определим энтропию выхода остатка из спирали. Для этого воспользуемся формулой (2.11). Учитывая, что в результате выхода остатка из цепи у него появляется 3 дополнительные степени свободы, и соответствующие координаты имеют по два устойчивых положения, число микросостояний системы возрастает в 2³ раз, тогда

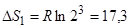( Дж·моль^-1·К^-1)

Учитывая, что энтропия величина аддитивная, энтропия плавления спирали равна

.

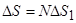Отсюда число остатков в цепи N = 20.

в) Учитывая, что на остаток в α-спирали приходится по 2 водородные связи (образуемые его N-H и C=O группами), энтальпия разрыва водородной связи равна 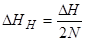, что составляет 2,8 кДж·моль^-1.