Термодинамика систем вдали от равновесия
Большинство процессов в природе не являются равновесными. Однако, почти любую систему вблизи равновесия можно разбить на физически бесконечно малые подсистемы, в которых локальное равновесие будет устанавливаться достаточно быстро.
Взаимодействие системы со средой происходит за счет обмена такими экстенсивными свойствами как объем, заряд, количество вещества - обобщенными координатами (q). Кроме того, взаимодействие возможно при наличии скалярного интенсивного свойства - обобщенной силы (F). Размерность силы зависит от размерности координаты, но произведение обобщенной силы на координату дает единицу энергии. Обобщенная работа является мерой взаимодействия системы со средой δA=Fdq.
Работа расширения
δA=pdV.
Электрическая работа по переносу заряда q, под действием разности потенциалов
δA=φdq.
Разность обобщенной силы между системой и средой является движущей силой самопроизвольных процессов переноса обобщенной координаты.
Энтропия является обобщенной тепловой координатой состояния, сопряженной с температурой — обобщенной силой, движущей силой переноса тепла.
Все обобщенные координаты, кроме энтропии, подчиняются закону сохранения, и могут изменяться только за счет обмена с внешней средой. Энтропия может возникать внутри системы за счет неравновесного процесса, в результате которого выделяется нескомпенсированная теплота δiQ, независимо от природы совершаемой работы. Связь теплоты с функцией состояния S позволяет охарактеризовать все многообразие неравновесных процессов в локально равновесной системе при помощи одной величины — энтропии S.
dS = deS + diS, (2.28)
где deS и diS изменение энтропии за счет обмена веществом и энергией с внешней средой и ее возникновение внутри системы.
Необратимые процессы можно описать на языке термодинамических сил (F) и потоков (X). Термодинамические силы (градиент температуры, потенциала, концентрации) вызывают потоки (теплоты, заряда, вещества). В общем случае
diS = F dX (2.29)
В случае потока теплоты F=(1/Tc -1/Th), где индексы c и h соответствуют низкой и высокой температуре.
Для потока вещества термодинамическая сила может быть выражена через химическое сродство (A). Для реакции X + Y « 2Y, Aº(mx+my-2mz). Химическое сродство является движущей силой химической реакции. Скорость увеличения энтропии выражается так:
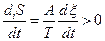 (2.30)
(2.30)
И в этом случае производство энтропии равно произведению термодинамической силы 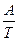 на термодинамический поток
на термодинамический поток 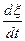 . Поток в этом случае есть превращение реагентов в продукты реакции, а
. Поток в этом случае есть превращение реагентов в продукты реакции, а 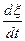 можно считать скоростью реакции (
можно считать скоростью реакции ( 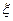 — степень полноты химической реакции:
— степень полноты химической реакции: 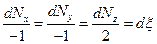 ). В равновесии А=0.
). В равновесии А=0.
В системе, в которой происходит химическая реакция и идет обмен теплом с окружающей средой, 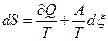 . Скорость изменения энтропии
. Скорость изменения энтропии
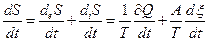 . (2.31)
. (2.31)
Локальная скорость возникновения энтропии отражает возникновение энтропии в неравновесном процессе в расчете на единицу объема:
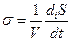 (2.32)
(2.32)
Локальная функция диссипации — это теплота, возникающая в неравновесном процессе:
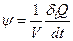 . (2.33)
. (2.33)
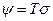 . (2.34)
. (2.34)
В линейной термодинамике неравновесных процессов принимается, что поток может зависеть от всех сил Jk=f(F1, F2, …, Fn), и постулируется линейная зависимость потоков от сил
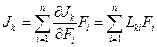 , (2.35)
, (2.35)
где 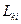 — это феноменологические коэффициенты Онзагера. Эта эмпирическая зависимость подтверждается многочисленными опытами (линейная связь тока и напряжения (закон Ома), теплового потока и градиента температуры (закон Фурье), потока вещества и градиента концентрации (закон Фика)).
— это феноменологические коэффициенты Онзагера. Эта эмпирическая зависимость подтверждается многочисленными опытами (линейная связь тока и напряжения (закон Ома), теплового потока и градиента температуры (закон Фурье), потока вещества и градиента концентрации (закон Фика)).
Основываясь на принципе микроскопической обратимости (инвариантность уравнений движения частиц относительно обращения направления времени), Онзагер получил соотношения, которые теперь носят его имя:
Lki=Lik.
Физический смысл соотношения в том, что сила Fj так влияет на поток Jk как и сила Fk на поток Ji. Примеры перекрестного влияния сил на потоки: нагревание вызывает возникновение потенциала (термопары, эффект Зеебака), термодиффузия (возникновение градиента концентраций под действием градиента температуры), электрофорез, ток течения и др. Применение соотношений Онзагера позволяет существенно редуцировать количество феноменологических коэффициентов.
Локальная функция диссипации линейно зависит от плотностей потоков и термодинамических сил (соотношение де Донде): 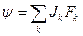 .
.
Транспорт воды и осмос
Рассмотрим применение формализма неравновесной термодинамики для описания потоков воды и их взаимодействия с потоками осмотиков. Осмотическое равновесие хорошо выполняется и большинство потоков и сил могут быть измерены непосредственно в эксперименте.
Рассмотрим взаимодействия потоков воды и незаряженного осмотика s для отдельной клетки в растворе. Мембрана отделяет внутреннюю среду (i) от наружной (o). Выходящие из клетки потоки принято считать положительными, а входящие — отрицательными.
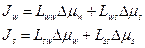 (2.36)
(2.36)
Удобнее вместо потока воды использовать объемный поток, равный сумме потоков воды и растворенного вещества 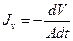 (м3 м-2 с-1), где А – площадь. Поток единственного осмотика
(м3 м-2 с-1), где А – площадь. Поток единственного осмотика 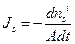 , (моль м-2 с-1). Согласно соотношению Онзагера Lsw=Lws. Пусть потоки вызваны только градиентом давления (или тургором, P) и градиентом концентрации (Csi-Cso) или разницей осмотического давления (Dps =RT(Csi-Cso)). Тогда выражения для потоков можно переписать через гидростатическое и осмотическое давление (вывод формул можно посмотреть в книге [4]) и они будут выглядят так:
, (моль м-2 с-1). Согласно соотношению Онзагера Lsw=Lws. Пусть потоки вызваны только градиентом давления (или тургором, P) и градиентом концентрации (Csi-Cso) или разницей осмотического давления (Dps =RT(Csi-Cso)). Тогда выражения для потоков можно переписать через гидростатическое и осмотическое давление (вывод формул можно посмотреть в книге [4]) и они будут выглядят так:
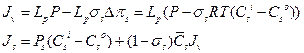
Из уравнения для Jv видно, что поток воды складывается из двух компонентов: гидравлического потока, вызванного разностью гидростатического давления (LpP, атмосферное давление принимают за ноль, Po=0), и осмотического потока, вызванного разностью осмотического давления (LpssDps). Осмотическая движущая сила направлена в противоположную сторону гидростатической силе, входит в уравнение со знаком минус и растет при накоплении осмотика внутри клетки (Csi>Cso). Гидравлическая проницаемость клеточной мембраны Lp связывает поток воды с соответствующей движущей силой—градиентом гидростатического давления. В осмотическом члене роль такого коэффициента выполняет Lpss. Физический смысл σs—пассивная селективность мембраны для данного осмотика. В случае идеальной полупроницаемой мембраны (пропускает воду, но не пропускает растворенное вещество) σs=1, и движущая сила для воды становится идентична разности водного потенциала 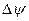 :
:
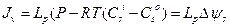 (2.37)
(2.37)
В случае равновесия (Jv=0) это уравнение идентично закону Ван-Гоффа P=RT(Ci—Co). Коэффициент отражения является количественной мерой отклонения поведения осмотической системы от идеальной полупроницаемой. Например, при σs = 0 мембрана не различает осмотик от растворителя (когда каналы большие, либо молекулы растворителя и растворенного вещества очень похожи). В реальных мембранах σs принимает значения от нуля до единицы. В некоторых случаях σs < 0. В этом случае клетка набухает при увеличении концентрации осмотика в среде. Это явление наблюдается в растительных клетках и получило название аномальный осмос. Можно рассматривать σs как степень взаимодействия воды с осмотиком при их транспорте через мембрану. Поскольку 0 < σs < 1, эффективная осмотическая движущая сила Dps снижается до σsDps. При σs =1 осмотическая и гидростатическая составляющие движущей силы создают одинаковые потоки воды через мембрану.
Обычно коэффициенты отражения для типичных осмотиков, присутствующих в клетке (соли, сахара, метаболиты) близки к единице и движущие силы можно заменить градиентом водного потенциала.
Уравнение для потока осмотика включает два члена. Первый член соответствует диффузионному потоку осмотика в соответствии с законом Фика. Коэффициент, связывающий движущую силу и поток в этом случае называется коэффициентом проницаемости (Ps). Второй член описывает взаимодействие воды и осмотика во время переноса через мембрану, например при вызванном потоком растворителя потоке вещества. 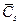 означает концентрацию осмотика в мембране (
означает концентрацию осмотика в мембране ( 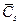 ~ (Csi-Cso)/2). В случае идеальной полупроницаемой мембраны (σs=1, Ps=0) второй член исчезает. С другой стороны, в случае совершенно неселективных барьеров (σs=0), этот член совпадет с конвекционным транспортом осмотика в потоке воды.
~ (Csi-Cso)/2). В случае идеальной полупроницаемой мембраны (σs=1, Ps=0) второй член исчезает. С другой стороны, в случае совершенно неселективных барьеров (σs=0), этот член совпадет с конвекционным транспортом осмотика в потоке воды.
Пример 2.8. Как и насколько изменится тургорное давление в клетке харовой водоросли при добавлении в наружный раствор непроникающего осмотика (соответствующее изменению осмотического давления наружного раствора Dpo)?
Решение: Клетка харовой водоросли представляет собой идеальный осмометр.
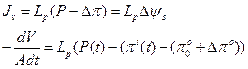
Используя определение коэффициента упругости клеточной стенки e, при небольших изменениях объема и тургора получаем:
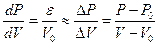 ,
,
где P0 и V0 начальные давление и объем.
Для идеального осмометра piV=p0iV0, и при малых изменениях объема получаем:
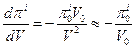
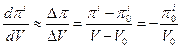
Тогда,
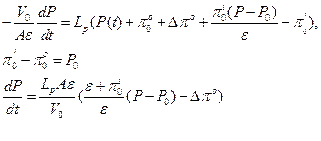
Интегрируя полученное уравнение при условии P=P0 при t=0; P=Pe при t=∞, получаем
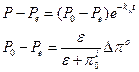 ,
,
где константа скорости транспорта воды через мембрану определяется выражением:
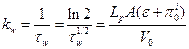
Таким образом, тургорное давление в клетке харовой водоросли увеличится до значения
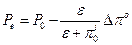 , по моноэкспоненциальному закону с постоянной времени
, по моноэкспоненциальному закону с постоянной времени 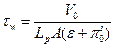 .
.
ЗАДАЧИ
2.1. Вычислить значение 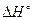 для реакции гидролиза мочевины (NH2)2CO до СО2 и NH3, катализируемой ферментом уреазой, если теплоты образования Н2Ожидк и мочевины, углекислого газа и NH3 в водных растворах составляют -287 кДж/моль, -320,5 кДж/моль, -414,5 кДж/моль, -81 кДж/моль, соответственно.
для реакции гидролиза мочевины (NH2)2CO до СО2 и NH3, катализируемой ферментом уреазой, если теплоты образования Н2Ожидк и мочевины, углекислого газа и NH3 в водных растворах составляют -287 кДж/моль, -320,5 кДж/моль, -414,5 кДж/моль, -81 кДж/моль, соответственно.
2.2.Известно, что при окислении одного моля глюкозы получается 38 молей АТФ. Оценить эффективность (в процентах) процесса окисления глюкозы, если известно, что для реакции сжигания С6Н12О6 DG˚= –2882 кДж/моль, а при синтезе одного моля АТФ из АДФ затрачивается31,4 кДж.
2.3.Изменение свободной энергии при молочнокислом брожении и при полном окислении глюкозы составляет -218 кДж/моль и -2882 кДж/моль, соответственно. Сколько молекул АТФ может быть синтезировано при распаде 1 молекулы глюкозы в анаэробных и аэробных условиях, если изменение свободной энергии реакции синтеза АТФ равно 31,4 кДж/моль и к.п.д. превращения энергии в клетке 100%.
2.4.Известно, что для реакции связывания АТФ с миозином ∆G с увеличением температуры от 273 до 285 К практически не изменяется. Определите ∆S этой реакции при 285 К, если ∆Н и ∆S при 273 К составляют -57,1 кДж/моль и -86 Дж/(моль∙К) соответственно, а ∆Н при 285 К -73,1 кДж/моль.
2.5.а) Вычислить изменение энтропии при нагревании 100 г воды от 0 до 15°С.
б) При какой температуре находилось 2 моль воды в сосуде, если при ее нагревании до 100°С энтропия увеличилась на 23,5 Дж/К?
в) Определить изменение энтропии в процессе таяния 1 моль льда при 0°С и последующем нагревании образующейся воды до 100°С.
г) Определить изменение энтропии в процессе превращения 1 моль воды в пар при температуре кипения и последующем нагревании пара до 150°С.
Удельная теплоемкость воды 4,190 Дж∙г-1∙К-1, удельная теплота плавления льда 333 Дж/г, удельная теплота парообразования 2260 Дж/г.
2.6.Получить выражение для химического потенциала одного моля идеального газа при постоянном объеме.
2.7.Молекулы N-метилацетамида, достаточно близкого аналога пептидного скелета, могут формировать водородную связь с участием амидной группы. Оцените, в каком растворителе ассоциация молекул N-метилацетамида термодинамически более выгодна, если известны данные, представленные в таблице:
| Растворитель | ΔH˚, кДж/моль | ΔS˚, Дж/(моль∙K) |
| CCl4 | -17,5 | -46 |
| Диоксан | -3,3 | -16,7 |
| H2O | 0,0 | -41,8 |
2.8.Для поддержания постоянной температуры тела человеческий организм теряет энергию путем испарения воды с поверхности тела. Какова масса воды, которую испаряет организм, если необходимо выделить 104 кДж энергии в день, образующейся в результате метаболических процессов? Удельная теплота испарения воды составляет 2,2 кДж/г.
2.9.Спортсмен массой 70 кг для поддержания постоянной температуры тела выделяет 600 кДж за один час тренировки. На сколько градусов изменилась бы температура тела за 1 час, если бы организм был изолированной системой? Принять теплоемкость тела равной 4,2 Дж∙г-1∙К-1.
2.10.Вычислите стандартную теплоту образования уксусной кислоты (в водном растворе) из простых веществ при 25°С, если известны значения 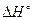 для следующих реакций:
для следующих реакций:
СН3COOHжидк+2O2 газ→2CO2 газ+2H2Oжидк 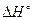 = -875 кДж/моль СН3COOHжидк,
= -875 кДж/моль СН3COOHжидк,
Сграфит+O2 газ→CO2 газ 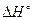 = -394,8 кДж/моль Сграфит,
= -394,8 кДж/моль Сграфит,
2Н2 газ+O2 газ→2H2Oжидк 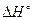 = -287 кДж/моль H2 газ.
= -287 кДж/моль H2 газ.
2.11.Рассчитайте средние значения энтальпий углерод−углеродных связей в этане С2Н6, этилене С2Н4 и ацетилене С2Н2, предполагая, что во всех этих соединениях энтальпия связи С−Н одинакова. Известны теплоты следующих реакций при стандартных условиях:
2Сграфит+3Н2 газ → C2H6 газ ΔН°=-20190 кал/моль
2Сграфит+2Н2 газ → C2H4 газ ΔН°=12555 кал/моль
2Сграфит+Н2 газ → C2H2 газ ΔН°=54230 кал/моль
Н2 газ → 2Hгаз ΔН°=104200 кал/моль
Сграфит → Cгаз ΔН°=171700 кал/моль
Сграфит+2Н2 газ → CH4 газ ΔН°=-17865 кал/моль.
Оцените относительную прочность одинарной, двойной и тройной углерод−углеродных связей.
2.12.Найдите работу Na+ -К+-АТФ-азы по переносу 3-х молей Na+ из клетки и 2-х молей К+ в клетку через плазматическую мембрану при 37°С, если их концентрации внутри клетки составляют 46 мМ и 340 мМ, а снаружи – 460 мМ и 10 мМ, соответственно. Потенциал на мембране = -60 мВ (φ внутри - φ снаружи).
2.13.Работа Na+ -К+-АТФ-азы по переносу 3-х молей Na+ из клетки и 2-х молей К+ в клетку через плазматическую мембрану при 37°С равна 40 кДж. Концентрации ионов Na+ и К+ внутри клетки составляют 15 мМ и 160 Мм, а снаружи - 150 мМ и 4 мМ, соответственно. Чему равен потенциал на мембране (φ внутри - φ снаружи)?
2.14.а) Определите рК ионизации уксусной кислоты при 298 К, если ∆Н° = -0,385 кДж/моль, ∆S° = -92,36 Дж/(моль·К)
б) Определите рК ионизации молочной кислоты при 298 К, если ∆Н° = -0,4 кДж/моль, ∆S° = -75,3 Дж/(моль·К)
в) Определите рК ионизации янтарной кислоты при 298 К, если ∆Н° = 3,2 кДж/моль, ∆S° = -69,8 Дж/(моль·К)
2.15.Для реакции фосфорилирования
глюкоза + Рi → глюкозо-6-фосфат
при рН = 7 и 37°C ∆G°' = 3 ккал/моль; концентрация фосфата и глюкозо-6-фосфата составляют 10-2 М и 10-4 М, соответственно. Оцените, какова возможная минимальная концентрация глюкозы, если ее фосфорилирование происходит за счет сопрягающей реакции гидролиза АТФ:
АТФ → АДФ + Рi
и для этой реакции в физиологических условиях ∆G' = -12 ккал/моль.
2.16.При 298 К для реакций
NAD+водн + пропанол-2водн ↔ NADHводн + ацетон водн + Н+ водн
пропанол-2 водн ↔ ацетон водн + Н2г
константы равновесия равны 7,71∙10-9 М и 5,27∙10-5 М, соответственно.
Найти константу равновесия для реакции
NAD+водн + Н2г ↔ NADHводн + Н+ водн.
2.17.Предположим, что в темноте концентрация АДФ и фосфата в хлоропластах составляет 2 мМ и 5 мМ, соответственно. Примем, что температура равняется 25°С, а рН близок к 7; для реакции фосфорилирования АДФ ΔG° = 30,6 кДж/моль. Какова концентрация АТФ при равновесии? При освещении хлоропластов концентрация АДФ за счет фосфорилирования уменьшается до 1 мМ. Определить концентрацию АТФ и изменение свободной энергии Гиббса при установившемся после освещения равновесии?
2.18.Если 10 мМ 3-фосфоглицерата смешать с фосфоглицеромутазой, катализирующей превращение этой кислоты в 2-фосфоглицерат (3-фосфоглицерат ↔ 2-фосфоглицерат), то при 37°С равновесная концентрация 3-фосфоглицерата станет равной 8,3 мМ, а 2-фосфоглицерата – 1,7 мМ. Как изменились бы равновесные концентрации, если бы первоначально внесли 1 М 3-фосфоглицерата? Определить константу равновесия для превращения 3-фосфоглицерата в 2-фосфоглицерат и величина ΔG° для этой реакции?
2.19.Найти ∆G' для реакции,
глюкоза + АТФ → глюкозо-6-фосфат + АДФ,
катализируемой гексокиназой при рН = 7 и 37°C, если известно, что отношение скоростей прямой и обратной реакции составляет 6,2∙106. В каком направлении реакция протекает самопроизвольно?
2.20.Найти отношение концентраций пирувата и фосфоенолпирувата для реакции,
фосфоенолпируват + АДФ → пируват + АТФ,
катализируемой пируваткиназой при рН 7 и 37°C, если известно, что ∆G°' этой реакции составляет –24,8 кДж/моль, концентрация АТФ в 2 раза больше концентрации АДФ и отношение скоростей прямой и обратной реакции составляет 3,9∙102.
2.21.Найти отношение скоростей прямой и обратной реакций
Фруктозо-6-фосфат + АТФ ↔ фруктозо-1,6-дифосфат + АДФ
катализируемой фосфофруктокиназой при рН 7 и 37°C, если известно, что ∆G' реакции составляет -25,2 кДж/моль.
2.22.Для реакции
фруктозо-1,6-дифосфат ↔ 2 глицеральдегид-3-фосфат,
катализируемой альдолазой при рН 7 и 37°C известно, что ∆G' реакции составляет -4,9 кДж/моль, а ∆G°' = 23,1 кДж/моль. Найти концентрацию глицеральдегид-3-фосфата, если концентрация фруктозо-1,6-дифосфата составляет 0,1 М.
2.23.В покоящейся мышце концентрации АТФ, АДФ и фосфата равны примерно 5, 1 и 10 Мм соответственно. Какова величина ΔG для гидролиза АТФ в этом случае, если ΔG°= -7,3 ккал/моль?
2.24.Найдите концентрацию АТФ в мышцах, если известно, что концентрация АДФ и фосфата в мышцах составляет 10-5 М и 10-3 М, соответственно, ∆G°' реакции синтеза АТФ при рН 7 и 310 К составляет 30,6 кДж/моль, а ∆G' = 59,67 кДж/моль.
2.25.Найти ∆G' реакции
гликогенn + Рi ↔ гликогенn-1 + глюкозо-1-фосфат,
при рН 7 и 37°C, если известно, что константа равновесия равна 0,3, концентрации фосфата и глюкозо-1-фосфата составляют 10 мМ и 0,03 мМ, соответственно, а концентрация гликогена практически не изменяется. В каком направлении реакция протекает самопроизвольно?
2.26.Найти ∆G°' реакции
пируват + NADH ↔ лактат + NAD
при рН=7 и 37°C, если в равновесии отношение концентраций NAD и NADH составляет 103, а отношение концентраций лактата и пирувата равно 10.
2.27.Дана последовательность реакций А↔В↔С. При 37°С даны константы равновесия КА↔В=0,73 и КВ↔С=1,64. Найти стандартную свободную энергию  ΔG° для этой системы реакций.
ΔG° для этой системы реакций.
2.28.Для реакции А + В ↔ С ΔG°= -17,8 кДж/моль при 37°С. Коэффициенты активности равны единице. В каком направлении будет протекать реакция при концентрации А, В и С равной 1мМ? Как изменится направление протекания реакции, если концентрация всех компонентов уменьшится до 1 мкМ?
2.28.ΔG° реакции полного окисления растворенной глюкозы до углекислого газа и воды составляет -2870 кДж/моль, а ΔG° реакции превращения АДФ в АТФ при стандартных состояниях всех компонентов реакции составляет 9,24 кДж/моль. Рассчитайте изменение свободной энергии при окислении 1 моль глюкозы и синтезе 1 моль АТФ при температуре 37˚С в условиях более близких к физиологическим:
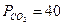 мм рт. ст.,
мм рт. ст.,
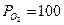 мм рт. ст.,
мм рт. ст.,
[глюкоза] = 1 мг/мл,
[АТФ] = [АДФ] = [Pi] = 1∙10-4 М,
рН = 7,0, активность воды принять равной 1.
Если при окислении 1 молекулы глюкозы образуется 38 молекул АТФ, какова эффективность процесса превращения энергии в клетке в условиях близких к физиологическим. Сравните с результатом задачи 2.2.
2.29.Во сколько раз изменится константа равновесия реакции при увеличении температуры от 25 до 37°С, если стандартная энтальпия реакции равна -88,7 кДж/моль.
2.30.На сколько изменится тургорное давление и объем клетки харовой водоросли, модуль упругости клеточной стенки которой равен 100 бар, а внутриклеточное осмотическое давление 7,3 бар, при добавлении в наружный раствор 50 мМ сахарозы (t = 20˚C).
2.31.Равновесное тургорное давление клетки Chara corallina (диаметр 1 мм) в искусственной прудовой воде (2 мосмоль/л) составляет 0,5 МПа. Модуль упругости клеточной стенки равен 100 бар. Время, за которое амплитуда приложенного небольшого импульса гидростатического давления уменьшается в 2 раза равно 4 с. T=20˚C. Чему равен коэффициент гидравлической проводимости мембраны этой водоросли?
2.32.Найти химическое сродство реакции X + Y « 2Z. Химический потенциал реагентов X и Y составляет 13 кДж/моль, а продукта Z 4 кДж/моль.
2.33.Раствор содержит два оптических изомера аминокислоты L и D. Начальные концентрации изомеров равны [L]0 и [D]0. Мономолекулярная константа скорости реакции рацемизации равна k (константа скорости реакции превращения L-изомера в D-изомер равна константе скорости обратной реакции). Получить зависимости от времени концентраций каждого из энантиомеров ([L] и [D]), химического сродства обратимой реакции рацемизации (A) и скорости производства энтропии ( 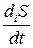 ), обусловленного протеканием реакции рацемизации, если температура раствора равна T.
), обусловленного протеканием реакции рацемизации, если температура раствора равна T.
2.34. Чему равно изменение энтропии в открытой системе, которая обменивается с окружающей средой теплотой Q=1250 кДж. За счет химических реакций в системе выделяется теплота 1750 кДж. Температура 27˚С. Найти общее изменение энтропии в системе.
2.35. Транспорт воды через полупроницаемые мембраны (проницаемые только для воды, но не для растворенных веществ) при наличии на мембране разности осмотического давления описывается уравнением
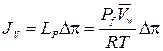 .
.
Здесь JV – объемный поток воды (объем воды, переносимый через единицу площади мембраны в единицу времени 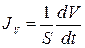 ), ∆π – разность осмотического давления на мембране,
), ∆π – разность осмотического давления на мембране, 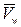 = 18 см3/моль – мольный объем воды, LP – гидравлическая проводимость мембраны и Pf – коэффициент осмотической водной проницаемости мембраны.
= 18 см3/моль – мольный объем воды, LP – гидравлическая проводимость мембраны и Pf – коэффициент осмотической водной проницаемости мембраны.
Суспензию эритроцитов в 250 мМ растворе сахарозы быстро смешали с более концентрированным раствором. Концентрация сахарозы после смешивания стала равной 350 мМ. Определить гидравлическую проводимость LP и коэффициент осмотической водной проницаемости мембраны эритроцита Pf при 37˚С, если через 700 мс после смешивания объем клеток уменьшился на 20%. Изменением концентрации сахарозы во внешнем растворе и площади поверхности эритроцита пренебречь. Отношение площади поверхности эритроцита начальному объему 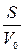 принять равным 13500 см−1. Сахароза через мембрану эритроцитов не проникает.
принять равным 13500 см−1. Сахароза через мембрану эритроцитов не проникает.
2.36.Мембрана растительной клетки непроницаема для сорбита. Плазмолиз в этой клетке начинается при концентрации сорбита в среде 0,4 М. Найти коэффициент отражения диметилформамида для мембраны, если известно, что с этим веществом плазмолиз начинается при концентрации 0,5 М? Считать, что объемные потоки в ходе плазмолитических экспериментов отсутствуют.
Дата добавления: 2015-06-22; просмотров: 3682;
