ЗАДАЧИ на разные темы

3.17.Кольцевая молекула с сопряженными связями. Рассмотрим молекулу бензола C₆H₆. Молекула бензола представляет собой плоскую кольцевую молекулу с сопряженными связями (см. введение). Примем для системы π-электронов молекулы модель кольцевой прямоугольной потенциальной ямы с бесконечно высокими стенками. Радиус кольца равен R, ширина кольца (ямы) равна d. Рассчитайте электронный энергетический спектр такой системы и оцените минимальную энергию поглощения (излучения), т.е. разность энергий между верхним занятым и нижнем свободным энергетическими уровнями.

3.18. Фактор Франка – Кондона. Здесь мы отвлечемся от прямоугольных потенциалов и обратимся к так называемым гармоническим потенциальным ямам. Мы не будем вдаваться в детали решения задачи о квантовом гармоническом осцилляторе, просто используем ее решение (интересующихся читателе мы переадресуем к [5] и [7]). 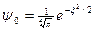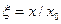Волновая функция основного состояния квантового гармонического осциллятора имеет вид , где - безразмерное отклонение осциллятора от положения равновесия 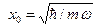- амплитуда нулевых колебаний осциллятора, m – масса осциллятора, ω – его частота. В теории электрон – колебательных взаимодействий есть так называемый фактор Франка – Кондона – интеграл перекрывания волновых функций нормальных гармонических осцилляторов молекулярной системы в двух электронных состояниях – до и после переноса электрона. В общем случае этот интеграл достаточно сложно вычисляется, но здесь мы рассмотрим один частный случай, который, однако, поможет понять простую суть этого фактора. Рассмотрим две одинаковые гармонические ямы, минимумы которых расположены на расстоянии 2d друг от друга (рис. 3.10).

Рис. 3.10. Изменение равновесного положения гармонического осциллятора (–d → +d) при изменении электронного состояния молекулярной системы.

В данном простом случае фактор Франка – Кондона определяется интегралом

,

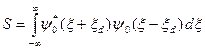где 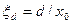- безразмерное положение равновесия осциллятора. Надо вычислить этот интеграл.

3.19.Рассчитать соотношение заселенностей правой и левой ям двухъямного потенциала. Рассчитать изменение энтропии. Минимумы потенциальных ям на одном уровне. Ямы различаются только шириной. Ямы считать параболическими (гармонический осциллятор), полная энергия системы много меньше высоты потенциального барьера. Использовать классический подход. Расчеты выполнить используя а)статистический подход и б) кинетический, т.е. используя связь свободной энергии процесса с константой равновесия и константами прямой и обратной реакций. Даны константы жесткости левой (k_A) и правой (k_B) парабол.

3.20. Получить приближенное выражение для времени диссипации кинетической энергии (порядка тепловой) частицы в вязкой среде, иначе говоря, время в течение которого частица «помнит» куда она двигалась. Оценить это время для глобулярного белка массой 70 кДа и диаметром 6 нм. Вязкость воды 10^-3 Па∙c.

3.21. Получить зависимость объема глобулы свободносочлененной цепи от числа звеньев.

3.22.Оценить максимальный электростатический потенциал на мембране, создаваемый мембранным фотосинтетическим центром. Расстояние между терминальными кофакторами электронного транспорта d — 30 Ǻ, разность их окислительно-восстановительных потенциалов ΔU — 0,7 В. Толщина мембраны D — 7 нм. Поле в мембране считать однородным.