Трансмембранные потоки ионов

Пассивное движение ионов через мембраны (без участия активных транспортных систем) происходит при наличии движущей силы – градиента электрохимического потенциала. Согласно основному уравнению электродиффузионной теории, ионный поток пропорционален движущей силе: 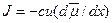, где c – концентрация иона в данной области, u – подвижность иона в данной среде, а 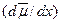– градиент электрохимического потенциала для данного вида ионов. Трансмембранный градиент электрохимического потенциала для ионов j представляют в виде:

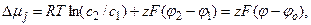(4.18)

где φ = φ₂ – φ₁ – мембранный потенциал, а 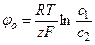– равновесный потенциал для данного вида ионов. Выражение 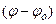характеризует движущую силу транспорта. Поток ионов J создает электрический ток I: 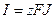. Коэффициент пропорциональности между величиной тока и действующей силой представляет собой проводимость g:

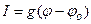(4.19).

В случае идентичного состава растворов с обеих сторон мембраны, проводимость для иона j равна:

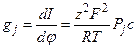, (4.20)

где Р_j – проницаемость мембраны для данного вида ионов, с – концентрация ионов, а φ – мембранный потенциал. Формула (4.20) описывает зависимость проводимости от концентрации проникающего электролита и проницаемости мембраны. Она не применима для описания изменений проводимости, связанных с переходами каналов между открытым и закрытым состояниями.

Для описания изменений проводимости потенциал-зависимых ионных каналов удобна кинетическая модель с двумя состояниями (закрытым и открытым), переходы между которыми зависят от мембранного потенциала с константами a и b , .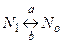

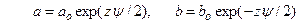В данной модели зависимость числа открытых состояний N_o от потенциала описывается сигмоидной (больцмановской) кривой

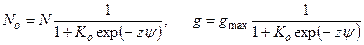, (4.21)

где N – общее число каналов, K_o = b_o/a_o – константа равновесия для переходов между двумя состояниями каналов при отсутствии мембранного потенциала, а ψ=φF/(RT) – мембранный потенциал в единицах RT/F (≈ 25 мВ при 20˚С).

Величина тока в системе потенциал-зависимых каналов определяется произведением общего числа каналов N, вероятности открытого состояния p=No/N, а также тока через одиночный канал i: 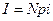, где i = g(φ – φ_o) – ток одиночного канала. Из уравнений (4.19, 4.21) видно, что изменения мембранного потенциала оказывают влияние как на движущую силу, так и на проводимость каналов. Поэтому, зависимость тока от напряжения на мембране в системе управляемых потенциалом каналов проявляет существенную нелинейность и может включать участок отрицательного наклона.

Участок с отрицательным наклоном характерен для возбудимых мембран. Такая вольт-амперная характеристика (ВАХ) появляется при условии, что область изменений проводимости g(φ), определяемая уравнением (4.21), сдвинута в сторону более отрицательных потенциалов по сравнению с равновесным потенциалом φ_o для данного вида ионов. Поэтому ВАХ для тока натриевых каналов (φ_o ~ +50 мВ) включает участок отрицательного сопротивления, а ВАХ для тока калиевых каналов в обычных условиях (φ_o < –100 мВ) не содержит участка отрицательного наклона.

Пример 4.7. Изобразить зависимость тока через Na канал от мембранного потенциала в интервале от –100 до 100 мВ при условии, что канал с проводимостью 5 пСм открывается при деполяризации мембраны до уровня φ > –50 мВ, а наружная и внутренняя концентрации Nа⁺ составляют соответственно 145 и 12 мМ. Температура 37°С.

Решение: В области –100 до –50 мВ канал закрыт, ток равен нулю. В области от –50 до 100 мВ зависимость линейна i = g(φ – φ_o), где φ_o=(RT/F)·ln(c_o/c_i)= 66,5 мВ. Положительные значения тока при φ > φ_o соответствуют выходящему направлению (из клетки в среду), а отрицательные токи при φ < φ_o соответствуют входящему току. При потенциале φ = 0 величинаNa⁺-тока составит i ≈ 5·10^–12 См·(–0,067 В) ≈ -0,33 пА. При потенциале открывания канала φ = –50 мВ, i ≈ 5·10^–12·(–0,05–0,067) ≈ -0,585 пА.

Суммарный ток, протекающий через мембраны, включает емкостную составляющую и ионный ток, состоящий из токов отдельных видов ионов: 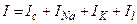, где I_l – ток утечки, для которого характерна линейная зависимость от напряжения на мембране. В физиологических условиях суммарный ток не выводится во внешнюю измерительную цепь и (при разомкнутой внешней цепи) равен нулю. В этих условиях ионный ток равен по абсолютной величине емкостному току.

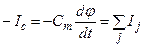(4.22)

Из (4.22) видно, что перенос ионов через мембрану вызывает изменение потенциала на мембране, представляющей диэлектрический слой (конденсатор) с емкостью С_m. В случае переноса определенного количества зарядов ΔQ (ΔQ = ∫I·dt) изменение напряжения Δφ составит:

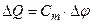(4.23)

Эта формула позволяет оценить мембранный потенциал, создаваемый при переносе известного количества зарядов, или же оценить минимально необходимый ионный поток сдвигающий напряжение на мембране в период потенциала действия. По данным о количестве перенесенных зарядов можно оценить изменения ионных концентраций.

Пример 4.8. Найти минимальное количество n молей Сa²⁺, которое необходимо перенести через поверхность мембраны нейрона (в расчете на 1 см²) для генерации потенциала действия с амплитудой 100 мВ. Емкость мембраны С_m = 1 мкФ/см². Насколько изменится внутриклеточная [Сa²⁺] при переносе найденного количества Са²⁺ во время потенциала действия в нейроне диаметром 50 мкм? При расчете допустить, что клетка – сферическая, а внутриклеточный уровень [Са²⁺] в покое составляет 100 нМ.

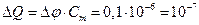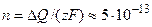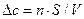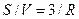Решение: Найдем заряд, который необходимо перенести через мембрану, чтобы сдвинуть потенциал на 100 мВ: Кл/см². Пересчитаем количество перенесенных зарядов на соответствующее количество молей вещества (z = 2) моль/см². Изменение концентрации внутри клетки при переносе внутрь количества Са²⁺, равного n, составит , где (см пример 4.1): 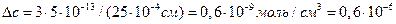М. Расчет показывает, что поток Са²⁺ во время потенциала действия вызывает многократное повышение исходного уровня Са²⁺.

Как видно из (4.22), емкость мембраны определяет скорость изменения мембранного потенциала за счет движения ионов по градиенту электрохимического потенциала. При подключении заряженного конденсатора C к резистору R в аналоговой модели мембраны, напряжение на конденсаторе снижается экспоненциально с постоянной времени τ = RC:

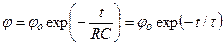. (4.24)

Поскольку удельная емкость биологических мембран С_m не претерпевает существенных изменений и составляет по разным оценкам от 0,5 до 1,0 мкФ/см², анализ кинетики релаксации мембранного потенциала хлоропластов после короткой заряжающей мембрану вспышки света позволяют оценить проводимость тилакоидных мембран в различных условиях (на свету и в темноте, при действии мембрано-активных агентов, при разных концентрациях ионов в среде):

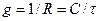(4.25)

Размерность правой части (4.25) – сименс: [Ф/с] = [Кл/(В с)] = [А/В] = [Ом^–1] = [См]. Во многих случаях размерности g и C отнесены к единице площади мембраны [Ф/см²] и [См/см²]. Сочетание (4.20) и (4.25) позволяет иногда оценивать проницаемость мембран по измерениям τ.

Пример 4.9. В приближении постоянного поля оценить удельные значения проводимости и сопротивления тилакоидной мембраны хлоропласта, окруженной растворами с одинаковым содержанием KCl (0,1 М), при условии, что основной вклад в проводимость связан с высокой проницаемостью мембран для К⁺ (Р_К = 4·10^-8 см/с). Какова постоянная времени мембраны t, если удельная емкость мембраны составляет 1 мкФ/см²?

Решение: Проводимость мембраны оценивают по формуле (4.20), а емкость – по (4.25):

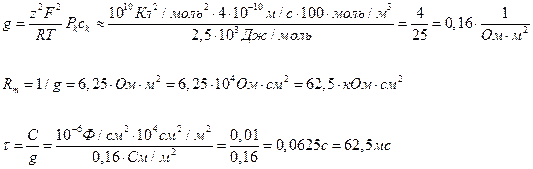
Пример 4.10. При измерениях кинетики спада индуцируемого вспышкой мембранного потенциала Δφ в тилакоидах хлоропластов найдено, что постоянная времени τ экспоненциальной кривой составляет после темновой адаптации хлоропластов 100 мс, а после предварительного освещения – 50 мс. В присутствии ингибитора Н⁺-АТФазы предварительное освещение хлоропластов не вызывало ускорения спада Δφ. Исходя из допущения, что снижение τ после предварительного освещения обусловлено активацией проводимости сопрягающего фактора CF₁-CF₀, оценить проводимость одиночного канала Н⁺-АТФазы и стационарный поток Н⁺ через одиночный канал при ΔрН ~ 3,3. Плотность расположения Н⁺-АТФаз в мембране тилакоидов составляет 0,2∙10^–13 моль/см².

Решение: Приращение проводимости, связанное по условию задачи с подключением на свету каналов Н⁺-АТФазы, составит:

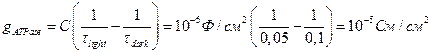
Проводимость одиночного канала Н⁺-АТФазы находим с учетом плотности расположения АТФаз и числа Авогадро (~6·10²³):

.

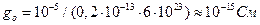Для оценки потока протонов выразим протондвижущую силу в единицах напряжения:

.

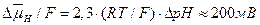Ток через одиночный канал составит 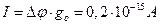, а количество переносимых H⁺ составит 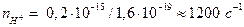. При стехиометрическом соотношении H⁺/АТФ = 3, поток H⁺ соответствует скорости синтеза АТФ ~ 400 c^–1 на один комплекс, что соответствует времени оборота фермента ~1/400 = 2,5 мс.