Электрохимические градиенты и преобразование энергии

Поддержание ионных градиентов на мембране позволяет совершать различные виды работы. Простейший пример – осмотическое поднятие воды за счет потока растворителя через полупроницаемую мембрану. Высота, на которую можно поднять жидкость, определяется разностью осмотических давлений между разделенными мембраной растворами. Осмотическое давление в случае, когда активности ионов или растворенных неэлектролитов примерно равны концентрациям (коэффициент активности близок к единице) выражается уравнением Вант-Гоффа

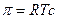. (4.30)

Пример 4.12. Оценить максимальную высоту поднятия воды в трубке, которая заполнена 0,01 М раствором KCl и отделена полупроницаемой мембраной от отсека с водой.

Решение: Пренебрегая отличиями активности ионов от концентраций, будем считать, что концентрация осмотически активных частиц (сумма катионов и анионов) равна 0,02 М. В условиях равновесия в осмотической ячейке, давление столба жидкости (отношение веса жидкости в трубке к площади сечения) равно осмотическому давлению: 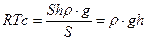. Отсюда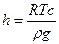

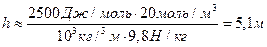
Один из механизмов вертикального подъема жидкости основан на молекулярных взаимодействиях, проявляющихся в виде поверхностного натяжения жидкости. Например, при погружении стеклянного капилляра воду, вода поднимается на различную высоту в зависимости от диаметра капилляра.

Пример 4.13. Найти высоту капиллярного поднятия воды в стеклянном капилляре радиусом 100 мкм. Угол смачивания (угол θ между мениском и стеклом) в случае воды равен нулю.

Решение: Сила, поднимающая воду в капилляре, равна ,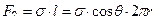

где σ – поверхностное натяжение (для воды 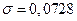Н/м), l – периметр мениска, а r – радиус капилляра. В условиях равновесия эта сила равна весу водного столба.

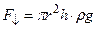. Из условия равенства сил получим

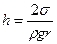(4.31)

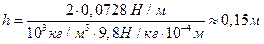
В биоэнергетике большую роль играет электрохимический градиент протонов, энергия которого используется для синтеза АТФ, выведения из клетки избытка ионов Na⁺ (что особенно важно для галотолерантных микроорганизмов) или вращения жгутиков. Электрохимический градиент протонов включает химическую и электрическую составляющие:

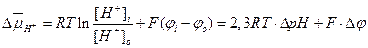, (4.32)

где ΔpH = pH_o – pH_i, а Δφ = φ_i – φ_o. Из (4.32) видно, что 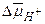выражается в Дж/моль.

Вместе с тем, электрохимический градиент протонов можно выразить в единицах напряжения или единицах рН:

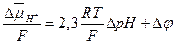, (В)

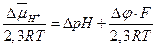, (ед. рН).

Пример 4.14. Оценить ЭДС АТР-зависимого Н⁺-насоса плазматической мембраны растительной клетки, т.е. максимально возможную разность потенциалов между цитоплазмой и средой (j_i - j_o), на основе термодинамических равновесных соотношений (энергия гидролиза АТP используется на транспорт Н⁺ из цитоплазмы в среду против 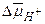). При расчете принять, что H⁺/ATP = 1 (для переноса одного протона используется энергия одной молекулы АТР), DG˚_ATP (стандартное изменение свободной энергии при гидролизе АТР) » -40 кДж/моль, отношение ATP/ADP в цитоплазме равно 10, [P_i] = 10 мМ, а значения рН среды (рН_о) и цитоплазмы (рН_i) составляют 6 и 8 ед. соответственно.

Решение:Запишем уравнение для сопряженных процессов гидролиза АТР и переноса протонов из цитоплазмы в среду:

ATP + H⁺_i = ADP + P_i + H⁺_o,

где H⁺_i и H⁺_o – протоны в цитоплазме и среде, соответственно.

Изменение термодинамического потенциала в ходе процесса будем считать равным нулю

.

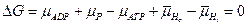Понижение энергии Гиббса в ходе гидролиза АТР компенсируется равным по величине возрастанием энергии при переносе протонов для поддержания .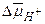

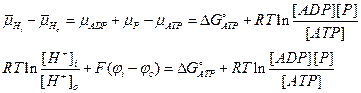
Из полученного выражения можно найти максимальную разность потенциалов :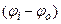

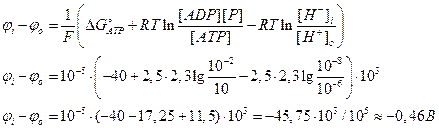
ЗАДАЧИ

4.1. Найдите среднюю величину смещения ‹x› молекулы формамида в воде и в растворе сахарозы за 1 мин, если коэффициенты диффузии этого вещества в воде и сахаразе составляют соответственно 1,6·10^–5 и 0,3·10^–5 см²/с.

4.2.Определите коэффициент диффузии эритрита в воде, если средняя величина смещения его молекулы составляет 40 мкм за 1 с.

4.3. Чему равен поток формамида через мембрану толщиной 8 нм, если коэффициент диффузии составляет 1,4·10^–8 см²/с, концентрация по одну из сторон мембраны равна 2·10^–4 М, а по другую сторону мембраны – в десять раз меньше?

4.4. Бислойная липидная мембрана (БЛМ) толщиной 10 нм разделяет два отсека, содержащих растворы метиленового синего в концентрациях 10^–2 и 2·10^–3 М. По изменениям окраски одного из растворов установлено, что поток красителя через БЛМ равен 3·10^–7 моль∙см^–2∙с^–1. Определите коэффициент диффузии метиленового синего в мембране.

4.5. Найдите коэффициент проницаемости плазматической мембраны для формамида, если разность концентраций этого вещества по разные стороны мембраны составляет 0,05 М, а поток через мембрану – 2,4·10^–8 моль·см^–2 с^–1.

4.6. Рассчитайте характерную толщину двойного электрического слоя для растворов NaCl с концентрациями 10^–5 и 10^–3 М.

4.7. Мембрана с плотностью отрицательных поверхностных зарядов 40 мКл/м² с каждой стороны окружена растворами KCl с концентрацией 10^–3 и 10^–1 М. Оценить внутримембранную разность потенциалов, создаваемую за счет разности поверхностных потенциалов.

4.8. Поверхностный потенциал мембраны равен –35 мВ. Найти рH у поверхности мембраны при условии, что рН в объеме среды составляет 7,6.

4.9. Во сколько раз отличается концентрация La³⁺ у поверхности заряженной мембраны от концентрации в растворе, если поверхностный потенциал составляет –30 мВ?

4.10. На поверхности мембраны протекает редокс реакция с участием заряженного редокс медиатора (акцептор А⁺) с валентностью z = +1 и находящегося в мембране донора D. Во сколько раз отличается истинная скорость реакции при высокой концентрации электролита (при φ_s = 0) от скорости реакции при φ_s = –25 мВ.

4.11. Оценить, насколько отличается плотность фиксированных зарядов s от максимального значения s_max для мембран из фосфатидилхолина при условии, что (а) среда содержит 10 мМ MgSO₄, j_s = -12,5 мВ, а константа связывания Mg²⁺ с мембранами составляет 1 М^-1, (б) среда содержит 10 мМ CaSO₄, j_s = -25 мВ, а константа связывания Ca²⁺ с мембранами составляет 100 М^-1.

4.12. В суспензию митохондрий добавлены одновалентные проникающие катионы и анионы до концентрации с_о = 10 мкМ. Оценить изменения концентрации катионного и анионного зондов в наружной среде при генерации в митохондриях мембранного потенциала –116 мВ при условии, что отношение объемов среды и митохондрий составляет V_o/V_i = 5·10³. Принять, что изменения наружной концентрации проникающих ионов обусловлены только их распределением в соответствии с мембранным потенциалом.

4.13. Изобразить зависимость тока I через K⁺-канал от мембранного потенциала j_m в интервале от –100 до 100 мВ при условии, что канал с проводимостью 20 пСм открывается при j_m > –50 мВ, а наружная и внутренняя концентрации K⁺ составляют соответственно 4 и 155 мМ. Отметить значения тока при j_m = 0. Температура 37˚С. Отметить положение точек пересечения графика с осями, если такие точки имеются.

4.14. Изобразить зависимость тока через Cl^--канал от мембранного потенциала j_m в интервале от –150 до 150 мВ при условии, что канал с проводимостью 10 пСм открывается при j_m > –50 мВ, а наружная и внутренняя концентрации Cl^– составляют соответственно 123 мМ и 4,2 мМ. Температура 37˚С.

4.15. Рассчитать равновесный потенциал для ионов Са²⁺ в мышечных волокнах млекопитающих при условии, что наружная концентрация Са²⁺ составляет 1,5 мМ, а внутренняя – 100 нМ.

4.16. Найти минимальное количество молей Na⁺, переносимого через 1 см² поверхности возбудимой мембраны, которое достаточно для генерации потенциала действия с амплитудой 100 мВ. Емкость мембраны принять равной 1 мкФ/см². Насколько изменится внутриклеточная концентрация Na⁺ во время потенциала действия в аксоне диаметром 500 мкм? В покое [Na⁺]_i= 10 мМ.

4.17. Рассчитать разность потенциалов Δφ, создаваемую на тилакоидной мембране при переносе одного электрона по ЭТЦ в ответ на короткую вспышку, если известно, что площадь участка S, занимаемого одной ЭТЦ, составляет 1,45·10^–11 см², а удельная емкость мембраны C_m = 0,5 мкФ/см². Примечание: площадь мембраны в расчете на одну ЭТЦ определена из данных о поверхности тилакоидных мембран – 1,75 м²/мг хлорофилла (1 мг ~10^–6 М Хл) и относительном содержании хлорофилла Р700 (Р700 : Хл = 1: 500). Плотность ЭТЦ в мембране составит 1,14^–13 моль Р700 на 1 см², а площадь S на одну ЭТЦ (1 молекула Р700) – 1,45·10^–11 см².

4.18. Рассчитать характерное время экспоненциального спада потенциала тилакоидной мембраны после световой вспышки в хлоропластах, обработанных валиномицином в среде с 0,1 М KCl, если проницаемость в присутствии ионофора составляет P_K = 4·10^–7 см/с, а C_m = 0,5 мкФ/см²

4.19. Какое количество одновалентных катионов в секунду проходит через неселективный канал, образованный антибиотиком аламетицином, если его проводимость g составляет 5 нСм, а потенциал на мембране ∆φ = 128 мВ?

4.20. Определите постоянную времени и характеристическую длину гигантского аксона кальмара, если удельное сопротивление аксоплазмы составляет 314 Ом·см, емкость и сопротивление мембраны – 1,1 мкФ/см² и 1570 Ом·см² соответственно, а диаметр аксона – 500 мкм.

4.21. Определите постоянную времени и характеристическую длину нервного волокна омара, если удельное сопротивление аксоплазмы составляет 173 Ом·см, емкость и сопротивление мембраны – 1,3 мкФ/см² и 2360 Ом·см² соответственно, а диаметр волокна – 75 мкм.

4.22. Определите постоянную времени и характеристическую длину мышечного волокна лягушки, если удельное сопротивление цитоплазмы составляет 418 Ом·см, емкость и сопротивление мембраны – 5 мкФ/см² и 4500 Ом·см², соответственно, а диаметр волокна – 45 мкм.

4.23. Две стеклянные пластинки, каждая шириной l расположены параллельно друг другу с зазором d = 0,2 мм. Если они вертикально погружены в воду при 20°С, на какую высоту h над поверхностью поднимется вода между пластинами? Поверхностное натяжение воды s = 0,0728 Н/м. Краевой угол смачивания θ = 0°.

4.24. Пластины плоского конденсатора погружены в воду. К пластинам прикладывают напряжение j. Замена воздуха на воду между пластинами приводит к понижению энергии системы. Поэтому вода втягивается в зазор до высоты h. Оценить высоту подъема воды при условии, что зазор d составляет 0,1 мм, а напряжение j = 100 В. Электрическую силу подъема воды можно найти как 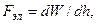где W =Сj²/2 – энергия заряженного конденсатора.

4.25. Определить разность электрохимических потенциалов 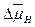на тилакоидной мембране хлоропласта для стационарного состояния, когда ΔрН = 3, а трансмембранный электрический потенциал Δφ равен 30 мВ.

4.26. Рассчитать величину ΔрH, создаваемого на тилакоидной мембране при действии короткой вспышки (перенос одного электрона по ЭТЦ), если известно, что буферная емкость тилакоидов составляет 0,18 моль Н⁺ на моль хлорофилла (Хл), а на одну ЭТЦ (на одну молекулу Хл Р700) приходится 500 молекул Хл.

4.27. Какое соотношение концентраций АТР/ADP может быть достигнуто в суспензии освещенных хлоропластов за счет ΔрН, равного 3 ед., и электрического потенциала Δφ = 20 мВ при концентрации фосфата в среде 10 мМ. Стандартное изменение термодинамического потенциала ΔG˚_ATP при синтезе ATP принять равным 32 кДж/моль, а стехиометрическое отношение n = Н⁺/АТР = 3.

4.28. Определить уровень 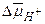на тилакоидной мембране освещенных изолированных хлоропластов, необходимый, чтобы отношение [ATP]/([АDP][P]) достигло значения 30000 M^–1. Принять, что отношение H⁺/АТР равно трем (n = 3), ΔG^°_ATP = 32 кДж/моль, а t = 25°C. Найти соответствующий уровень ΔpH, если Δφ = 30 мВ.

4.29. Транспорт воды через полупроницаемые мембраны (проницаемые только для воды, но не для растворенных веществ) при наличии на мембране разности осмотического давления описывается уравнением

.

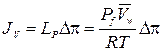Здесь J_V – объемный поток воды (объем воды, переносимый через единицу площади мембраны в единицу времени 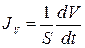), ∆π – разность осмотического давления на мембране, 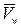= 18 см³/моль – мольный объем воды, L_P – гидравлическая проводимость мембраны и P_f – коэффициент осмотической водной проницаемости мембраны.

Суспензию эритроцитов в 250 мМ растворе сахарозы быстро смешали с более концентрированным раствором. Концентрация сахарозы после смешивания стала равной 350 мМ. Определить гидравлическую проводимость L_P и коэффициент осмотической водной проницаемости мембраны эритроцита P_f при 37˚С, если через 700 мс после смешивания объем клеток уменьшился на 20%. Изменением концентрации сахарозы во внешнем растворе и площади поверхности эритроцита пренебречь. Отношение площади поверхности эритроцита начальному объему 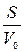принять равным 13500 см⁻¹. Сахароза через мембрану эритроцитов не проникает.

4.30. Цианиновые красители используются как флуоресцентные зонды для определения мембранного потенциала клеток. Молекулы цианиновых красителей заряжены положительно и накапливаются в цитоплазме клеток при отрицательном мембранном потенциале. Накопление красителя в цитоплазме приводит к концентрационному тушению флуоресценции. Таким образом, создание положительного потенциала внутри приводит к усилению флуоресценции, а отрицательного – к ее тушению.

Для определения мембранного потенциала эритроцитов к суспензии клеток добавили цианиновый флуоресцентный зонд diS-C₃-(5). После установления стационарного уровня флуоресценции к суспензии эритроцитов добавили ионофор валиномицин, значительно повышающий проницаемость мембраны для ионов K⁺. Если среда, в которой находились клетки, содержала 102 мМ K⁺, то после добавления валиномицина интенсивность флуоресценции не менялась. Если среда содержала 153 мМ K⁺, флуоресценция возрастала, а если 51 или 0 мМ K⁺ – она убывала. Определить величину потенциала на эритроцитарной мембране до добавления ионофора при 37˚С, если в цитоплазме концентрация K⁺ равна 153 мМ. В отсутствие валиномицина мембрана эритроцитов плохо проницаема для катионов.

4.31. Ионофор нигерицин переносит через мембрану один ион K⁺ в обмен на один ион H⁺. Нигерицин используют, чтобы уравнять величину pH в цитозоле клеток и во внешней среде. Для этого клетки помещают в среду, где концентрация ионов K⁺ равна концентрации этих ионов в цитозоле клеток и добавляют ионофор. Показать, что в этой системе после установления равновесия величина pH цитозоля сравняется с величиной pH среды. Какой будет разница величин pH цитозоля и внешней среды после добавления нигерицина, если концентрация K⁺ в среде будет в 10 раз меньше концентрации в цитозоле?

4.32. Na⁺/K⁺-АТФаза – фермент, который осуществляет активный транспорт одновалентных катионов через клеточную мембрану. За один цикл работы фермента из клетки выводится три иона Na⁺ в обмен на два иона K⁺. В стационарном состоянии поток иона, создаваемый ферментом полностью компенсируются пассивным потоком утечки, обусловленным мембранной проницаемостью. Используя приближение постоянного поля для токов утечки, показать, что стационарный потенциал, возникающий на мембране при работе Na⁺/K⁺-АТФазы, можно рассчитать с помощью уравнения Томаса:

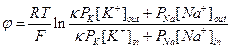
где P_K и P_Na – проницаемость мембраны для ионов K⁺ и Na⁺ соответственно, κ = 3/2. Индексы in и out относятся к цитоплазме и внешней среде.