Кабельные свойства волокон

Механизм распространения потенциала действия по нервному волокну включает стадию электротонического распределения потенциала, аналогичного распределению потенциала в электрическом кабеле. Если один из участков аксона деполяризован, возникают локальные токи, которые вызывают деполяризацию соседних участков и смещают потенциал в сторону достижения порогового уровня. Распространение токов описывается кабельным уравнением. Продольный ток описывается законом Ома: 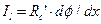, где dφ/dx – разность потенциалов на единицу длины волокна, а R_c´ – сопротивление цитоплазмы на единицу длины волокна. В стационарном состоянии емкостной ток через мембрану равен нулю (I_C = C_m·dj/dt = 0). В этих условиях трансмембранный ток на участке аксона длиной dx равен убыли продольного тока на этом же участке: φ/R_m´= dI_l/dx, где R_m´ – сопротивление мембраны на единицу длины волокна:

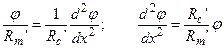(4.26)

Решение уравнения имеет вид

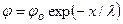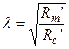, где (4.27)

Значения R_m´ и R_c´ зависят от геометрических параметров волокна. Чем шире сечение волокна, тем ниже сопротивление цитоплазмы и тем больше площадь мембранной поверхности в расчете на единицу длины волокна. С увеличением длины сегмента волокна сопротивление столба цитоплазмы возрастает, а сопротивление окружающей его мембраны, напротив, снижается (т.к. поверхность мембраны увеличивается). Поэтому размерности R_m´ и R_c´ существенно различаются.

Сопротивление проводника с сечением S и длиной l описывается «школьной» формулой 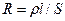. Сопротивление проводника (столба аксоплазмы) на единицу длины равно 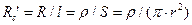, где r – радиус волокна. Из приведенной формулы видно, что R_c´ имеет размерность Ом/см.

Сопротивление мембраны также подчиняется формуле 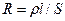, где ρ – удельное сопротивление материала мембраны, l – толщина мембраны, а S – площадь её поверхности. Поскольку толщина мембраны постоянна, произведение 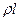обозначают R_m и называют удельным сопротивлением мембраны, т.е. 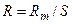. В случае волокна цилиндрической формы поверхность мембраны 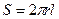, а сопротивление мембраны для участка произвольной длины равно 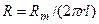. Сопротивление мембраны в расчете на единицу длины составит 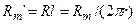. Отсюда видно, что R_m´ имеет размерность Ом·см, а размерность λ в (4.27) – сантиметры.

Суммируя промежуточные результаты, можем записать

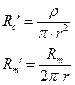(4.28)

При подстановке (4.28) в (4.27) находим, что константа длины λ возрастает с увеличением удельного сопротивления мембраны и с понижением сопротивления аксоплазмы, а также возрастает пропорционально корню квадратному из радиуса волокна:

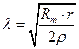(4.29)

Пример 4.11. Удельное сопротивление плазматической мембраны R_m длинной цилиндрической клетки (волокна) составляет 30 кОм·см², а удельное сопротивление внутренней среды r = 1 кОм·см. Оценить постоянную длины волокна l для клетки с диаметром d (а) 1 мм и (б) 100 мкм.

Решение: Используя соотношения (4.26-4.28), находим значения константы длины λ:

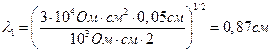; λ₂ = 0,27 см