Диффузия ионов и неэлектролитов
Диффузия представляет собой спонтанное движение растворенного вещества в сторону понижения концентрации. Диффузионные законы определяют движение незаряженных веществ в объеме (на любых расстояниях при отсутствии конвекции), перенос ионов в неперемешиваемых слоях у поверхности мембран, а также движение ионов на малых расстояниях.
Формула Стокса–Эйнштейна связывает коэффициент диффузии D с температурой T, вязкостью среды η и радиусом диффундирующих частиц r (k – константа Больцмана). Например, вязкость воды при 20°С составляет ηH2O= 10–3 Па∙с (1 Па = 1 Н/м2).
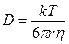 (4.1)
(4.1)
Пользуясь (4.1), можно оценить коэффициент диффузии в воде для малых молекул с радиусом ~0,2 нм (10–5 см2/с) или для молекул другого размера. На движение ионов в растворе влияет электрическое поле. Коэффициент диффузии иона зависит от его заряда (z):
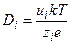 , (4.2)
, (4.2)
где u – подвижность иона, имеющая размерность м2·с–1·В–1 (см2·с–1·В–1), е – заряд электрона. Например, подвижности ионов K+ и Na+ равны 7,6·10–4 и 5,2·10–4 см2·с–1·В–1, соответственно. Из (4.1) и (4.2) получаем уравнение для расчета подвижности иона по его радиусу и заряду.
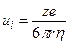 (4.3)
(4.3)
Подвижность численно равна скорости движения ионов (см/с) при напряженности поля 1 В/см.
Законы Фика описывают скорость диффузии вещества, а также пространственное распределение концентрации диффундирующего вещества в различные моменты времени.
Первый закон Фика связывает поток вещества J с коэффициентом диффузии D и градиентом концентрации (dc/dx). Размерность потока – моль∙см–2∙с–1).
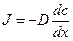 (4.4)
(4.4)
В случае диффузии через тонкую мембрану
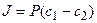 , (4.5)
, (4.5)
где P=Dg/h – проницаемость, h – толщина мембраны, g – коэффициент распределения вещества между водной и липидной фазами, а 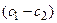 – разность концентраций диффундирующего вещества в объемных фазах по разные стороны мембраны.
– разность концентраций диффундирующего вещества в объемных фазах по разные стороны мембраны.
Второй закон Фика описывает направление изменений концентрации вещества во времени (dc/dt) в зависимости от знака второй производной (d2c/dx2), определяющей вогнутость или выпуклость профиля концентрации по координате x:
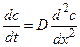 (4.6)
(4.6)
Из (4.6) в частности следует, что в случае одномерной стационарной диффузии (т.е. при dc/dt=0) профиль концентрации линеен: 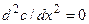 . В общем случае одномерной диффузии пространственно-временное распределение вещества описывается нормальным распределением Гаусса:
. В общем случае одномерной диффузии пространственно-временное распределение вещества описывается нормальным распределением Гаусса:
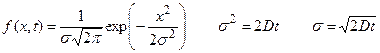 (4.7)
(4.7)
где x – координата, f(x,t) – функция распределения, σ – среднеквадратичное отклонение для нормального распределения вещества относительно исходной точки при x = 0, σ2 – дисперсия, а t – время. Область, расположенная между координатами ±σ, содержит более 68% от общего количества диффундирующего вещества. Согласно уравнению Эйнштейна, величина σ, обозначаемая также 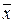 или ‹x›, служит мерой расстояния, на которое распространяется диффундирующее вещество за определенный промежуток времени t:
или ‹x›, служит мерой расстояния, на которое распространяется диффундирующее вещество за определенный промежуток времени t:
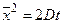 , (4.8)
, (4.8)
где 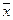 – среднеквадратичное отклонение (диффузионная длина).
– среднеквадратичное отклонение (диффузионная длина).
Пример 4.1. После инъекции в клетку некоторого вещества до концентрации co, клетку отмывают средой, не содержащей этого вещества. Какое время инкубации необходимо, чтобы внутренняя концентрация вещества понизилась в 10 раз, если проницаемость мембраны для этого вещества составляет 10–4 см/с? Решить задачу для клетки сферической формы с диаметром 200 мкм и для цилиндрической клетки с диаметром 200 мкм и длиной 1 см.
Решение: При записи первого закона Фика учтем, что диффузия происходит через тонкую мембрану и, что концентрация во внешнем растворе равна нулю.
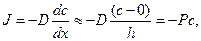 где с – концентрация вещества в клетке в момент времени t. Зная поток вещества через мембрану и геометрию клетки (площадь поверхности S и объем V), можно выразить изменение внутренней концентрации dc за промежуток времени dt:
где с – концентрация вещества в клетке в момент времени t. Зная поток вещества через мембрану и геометрию клетки (площадь поверхности S и объем V), можно выразить изменение внутренней концентрации dc за промежуток времени dt:
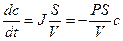 .
.
Решение этого дифференциального уравнения описывает кинетику изменения концентрации вещества внутри клетки:
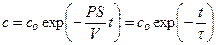 , где
, где 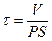 .
.
Уравнение решают методом разделения переменных и интегрирования по времени от нуля до t при соответствующем изменении концентрации от co до c.
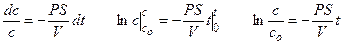
Для ответа на вопрос задачи удобно перейти к десятичным логарифмам:
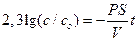
Отношение S/V определяется геометрией клетки. Для сферы и цилиндра оно составляет соответственно
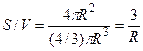 и
и 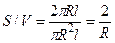 .
.
С учетом условия задачи c/co = 0,1 и R = 0,01 см, находим искомое время t:
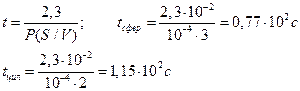
Аналогичный подход используется для случаев, когда в момент времени t = 0 в наружный раствор добавляют проникающее вещество, которое начинает поступать внутрь клетки, причем наружная концентрация остается постоянной (co = const) из-за большого объема среды по сравнению с объемом клеток. В таком опыте моменту времени t = 0 соответствует внутренняя концентрация с = 0, а произвольному моменту времени t соответствует внутренняя концентрация с. В этом случае интегрирование дифференциального уравнения приводит к следующему решению:
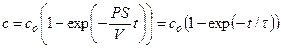 .
.
Пример 4.2. Предположим, что через калиевый канал с устьем R = 10 Å протекает ток I силой 10 пА (рис. 4.1.). При этом концентрация К+ в устье повышается по сравнению с объемом раствора. Найти концентрацию в области устья канала, если концентрация К+ в объеме составляет 10 мМ. При расчете принять, что коэффициент диффузии К+ в воде ~10-5 см2/с.
Рис. 4.1.
Решение: На выходе из канала суммарный поток переносимых ионов диффундирует во всех направлениях, ограничиваемых полусферой. Выделим элемент поверхности полусферы и запишем поток через единицу поверхности, пользуясь первым законом Фика.
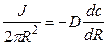
Суммарный поток вещества J связан с электрическим током I соотношением 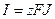 , где F – число Фарадея. Отсюда получим
, где F – число Фарадея. Отсюда получим
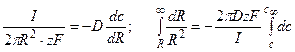
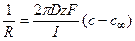 , где z =1
, где z =1
Следовательно, перепад концентрацией между устьем канала и объемом раствора составит
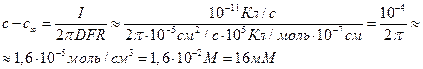
Соответственно, концентрация в устье канала cx составит 26 мМ.
Пример 4.3. Концентрация Са2+ в питательном растворе на расстоянии 300 мкм от поверхности корня составляет 100 мкМ, а у поверхности корня с диаметром 200 мкм – 80 мкМ. Оценить диффузионный поток Са2+ к поверхности корня на 1 см его длины (моль·с–1), а также поток Са2+ на единицу поверхности корня (моль·см–2·с–1) в предположении, что коэффициент диффузии D = 5·10–6 см2/с.
Решение: Обозначим суммарный диффузионный поток для сегмента корня длиной l символом J0. Поток Са2+ направлен радиально из объема среды к центру корня. Поток через единичный участок цилиндрической поверхности неперемешиваемого слоя на расстоянии R от центра корня составит J0/(2πRl). Запишем уравнение первого закона Фика в радиальных координатах:
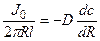
Решая уравнение, находим формулу для расчета потока по концентрациям на разном удалении от центра корня (концентрации с1 и с2 для радиальных расстояний R1 и R2).
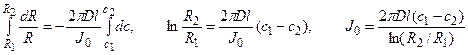
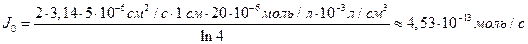
В расчете на единицу поверхности корня поток составит
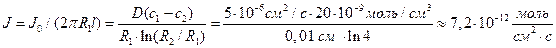 .
.
Дата добавления: 2015-06-22; просмотров: 3296;
