Ионные равновесия
Представления о равновесных потенциалах для отдельных видов ионов занимают важное место в электрофизиологии животных и растительных клеток. Равновесный потенциал φj для вида ионов j вычисляют по формуле Нернста, которая выводится из условия равенства электрохимических потенциалов в растворах по разные стороны от мембраны, например, внутри и снаружи клетки:
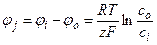 , (4.9)
, (4.9)
где 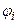 и
и 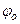 – электрические потенциалы внутри клетки и в наружной среде в условиях электрохимического равновесия, а co и ci – концентрации данного иона снаружи и внутри клетки. Чем больше отклонение мембранного потенциала от равновесного потенциала, тем большая движущая сила действует на ион. Величина этого отклонения представляет собой разность электрохимических потенциалов, выраженную в единицах напряжения (
– электрические потенциалы внутри клетки и в наружной среде в условиях электрохимического равновесия, а co и ci – концентрации данного иона снаружи и внутри клетки. Чем больше отклонение мембранного потенциала от равновесного потенциала, тем большая движущая сила действует на ион. Величина этого отклонения представляет собой разность электрохимических потенциалов, выраженную в единицах напряжения ( 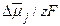 ). В линейном приближении поток пропорционален действующей силе:
). В линейном приближении поток пропорционален действующей силе:
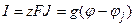 , (4.10)
, (4.10)
где I – электрический ток создаваемый потоком J ионов с валентностью z, F – число Фарадея, а g – проводимость канала или мембраны для данного вида ионов. Для многих животных клеток мембранный потенциал приближается к величине равновесного калиевого потенциала. Однако распределение ионов Na+ и Ca2+ между клеткой и средой резко отличается от равновесного. Для растительных клеток характерно неравновесное распределение ионов Ca2+, Cl– и H+.
Термодинамические равновесные соотношения используют также для описания распределения ионов в двойном электрическом слое, величины поверхностного заряда мембран, а также распределения ионов в доннановской системе. Доннановская ячейка представляет собой термодинамически равновесную систему из двух компартментов, которые разделены мембраной, проницаемой для простых неорганических ионов но непроницаемой для крупных молекул полиэлектролитов (например, белков). Аналогичное равновесие возникает и при отсутствии мембраны, если одна из контактирующих фаз (полиэлектролитный гель или пористый материал) содержит фиксированные заряды, неспособные перейти в водный раствор. Для свободно распределяющихся ионов (как для катионов, так и для анионов) выполняется уравнение Нернста, причем в чистом водном растворе концентрации катионов и анионов одинаковы и равны с. Записав уравнение (4.9) отдельно для катионов и анионов и приравняв разность потенциалов, получим с+ · с– = с2, где с+ и с– – концентрации катионов и анионов в заряженной фазе. В фазе, содержащей полиэлектролит, концентрации свободных катионов и анионов различаются, т.к. должно соблюдаться условие электронейтральности данной фазы: 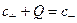 , где Q – общая концентрация фиксированных положительных зарядов. Объединяя приведенные формулы, получаем квадратное уравнение, которое описывает концентрацию катионов в заряженной фазе в зависимости от концентрации фиксированных зарядов Q и концентрации электролита в водной фазе:
, где Q – общая концентрация фиксированных положительных зарядов. Объединяя приведенные формулы, получаем квадратное уравнение, которое описывает концентрацию катионов в заряженной фазе в зависимости от концентрации фиксированных зарядов Q и концентрации электролита в водной фазе:
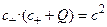 (4.11)
(4.11)
Решения этого квадратного уравнения упрощаются для частных случаев с+<<Q и c+>>Q.
Пример 4.4. Растворы разделены мембраной, проницаемой для ионов, но непроницаемой для белка. Первый раствор содержит 30 мМ белка, молекулы которого несут заряд, равный –1, второй – 36 мМ NaCl. Определите разность потенциалов на мембране и концентрацию ионов Na+ и Cl– в первом растворе (t = 27˚C).
Решение: Условие электронейтральности заряженной фазы по условию задачи имеет вид 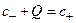 . С учетом соотношения с+·с–= с2 получим
. С учетом соотношения с+·с–= с2 получим 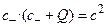 . Решая квадратное уравнение, находим с–.
. Решая квадратное уравнение, находим с–.
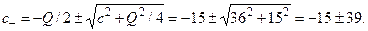
Из двух решений годится только положительное: с– = 24 мМ. Отсюда с+ = 54 мМ. Разность потенциалов Δφ составит
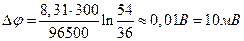 .
.
Один из распространенных примеров ионного равновесия – равновесие в двойном электрическом слое. Концентрация ионов с валентностью z вблизи мембраны, несущей отрицательные фиксированные заряды, описывается уравнением Больцмана:
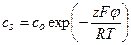 , (4.12)
, (4.12)
где φ – потенциал в данной точке двойного слоя относительно потенциала в объеме раствора, а co – концентрация иона данного вида в объеме. Очевидно, что различия между концентрациями cs и co (у поверхности мембраны и в объеме среды) возрастают с увеличением валентности иона и величины φ, зависящей от плотности фиксированных зарядов.
В теории двойного электрического слоя существует понятие длины экранирования. Длина экранирования соответствует расстоянию, при котором электрический потенциал относительно объема раствора снижается в е раз (е - основание натуральных логарифмов) по сравнению с поверхностным потенциалом. Длина экранирования обратно пропорциональна корню квадратному из концентрации электролита в растворе с:
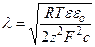 , (4.13)
, (4.13)
где ε – относительная диэлектрическая проницаемость воды (~81), а εo – абсолютная диэлектрическая проницаемость вакуума εo ≈ 8,85∙10–12 Ф/м. Эта формула позволяет оценивать толщину двойного электрического слоя при разных концентрациях электролита в растворе.
Связь между плотностью фиксированных зарядов на мембране, поверхностным потенциалом и концентрацией электролита в растворе описывается уравнением Гуи–Чапмена:
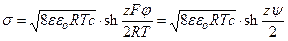 , (4.14)
, (4.14)
где ψ=Fφ/(RT) – поверхностный потенциал в безразмерных единицах, sh – функция гиперболический синус ( 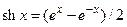 ), а z = 1 для бинарных электролитов типа NaCl и z = 2 для солей типа СаSO4. В случае малых потенциалов shx ≈ x. В этом случае можно считать, что поверхностный потенциал мембраны пропорционален плотности фиксированных зарядов и обратно пропорционален корню квадратному из концентрации электролита:
), а z = 1 для бинарных электролитов типа NaCl и z = 2 для солей типа СаSO4. В случае малых потенциалов shx ≈ x. В этом случае можно считать, что поверхностный потенциал мембраны пропорционален плотности фиксированных зарядов и обратно пропорционален корню квадратному из концентрации электролита:
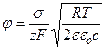 . (4.15)
. (4.15)
Одно из важных предположений в теории Гуи–Чапмена состоит в том, что плотность фиксированных зарядов σ не зависит от концентрации электролита в окружающем мембрану растворе. Это допущение оправдано лишь в случаях низкой константы связывания ионов с мембраной или же низкой концентрации электролита. Система уравнений, включающая (4.14) и учитывающая изменения σ при связывании ионов с мембраной, существенно расширяет область применения теории двойного слоя Гуи–Чапмена. Связывание катионов М+ с мембраной можно рассматривать как их обратимое взаимодействие с фиксированными отрицательными зарядами A– с константой связывания K: 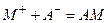 . Заряд σ при таком связывании снижается
. Заряд σ при таком связывании снижается
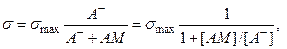 (4.16)
(4.16)
где А– и АM связаны соотношением
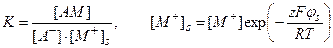 . (4.17)
. (4.17)
Концентрация [M+]s на границе с мембраной отличается от объемной концентрации [M+].
Поверхностный заряд и поверхностный потенциал играют важную роль в биологических процессах. Электростатическое притяжение протонов к фиксированным отрицательным зарядам мембраны вызывает локальное понижение рН у поверхности мембраны по сравнению с рН в объеме раствора. Поскольку рН у поверхности отличается от объемного значения, истинные константы диссоциации ионизируемых групп не совпадают с кажущимися константами. Наличие поверхностного заряда влияет на скорость окислительно-восстановительных процессов, протекающих с участием заряженных редокс медиаторов. Значения поверхностного, а также дипольного потенциала определяют высоту электростатического барьера, преодолеваемого ионами при прохождении через мембраны, и, следовательно, существенно влияют на проводимость мембран. Разность поверхностных потенциалов для двух сторон мембраны может создавать внутримембранное электрическое поле, которое оказывает влияние на процессы прямого и обратного переноса электронов в реакционных центрах фотосинтетических мембран, на степень активации ионных каналов, электростатическое сжатие мембраны и устойчивость мембран к электрическому пробою. Поверхностные потенциалы являются одним из основных факторов, определяющих равновесное расстояние между параллельно ориентированными мембранами (стыковка и расхождение тилакоидов в хлоропластах).
Пример 4.5. При добавлении 0,1 M KCl к тилакоидам, находящимся в бессолевой среде, наблюдали такие же изменения светорассеяния препаратов, как и при добавлении 0,01 М MgSO4. Пользуясь теорией двойного электрического слоя оценить плотность поверхностных зарядов на тилакоидной мембране и величину поверхностного потенциала, создаваемого при указанных воздействиях.
Решение: Одинаковый уровень светорассеяния препаратов в средах с KCl и MgSO4свидетельствует об одинаковой упаковке тилакоидов в гранах, что достигается при равенстве поверхностных потенциалов для двух указанных воздействий. Согласно теории Гуи–Чапмена, плотность поверхностных зарядов s постоянна и при постоянном рН не зависит от природы электролита. Из условия задачи следует, что j1 = j2, где j1 и j2 – поверхностные потенциалы, создаваемые в присутствии солей одновалентных и двухвалентных ионов (KCl и MgSO4, соответственно). Запишем формулу (4.14) для каждого из этих электролитов и приравняем значения s, а также учтем, что y1 = y2 = y. Получим
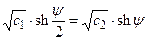 , где ψ=Fφ/(RT), а с1 и с2 – концентрации солей одно- и двухвалентных ионов. Функцию sh ψ в правой части можно представить как разность квадратов и сократить на sh ψ/2. При этом получим
, где ψ=Fφ/(RT), а с1 и с2 – концентрации солей одно- и двухвалентных ионов. Функцию sh ψ в правой части можно представить как разность квадратов и сократить на sh ψ/2. При этом получим
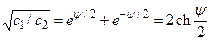 ;
;
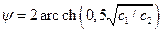 ≈ 2,06; φ ≈ 2,06∙25 мВ= 51,6 мВ. Знак поверхностного потенциала – отрицателен в соответствии с отрицательным знаком σ. Пользуясь (4.14), рассчитаем σ:
≈ 2,06; φ ≈ 2,06∙25 мВ= 51,6 мВ. Знак поверхностного потенциала – отрицателен в соответствии с отрицательным знаком σ. Пользуясь (4.14), рассчитаем σ:
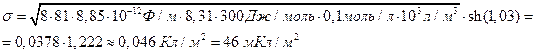
При проведении расчетов можно избежать применения прямых и обратных гиперболических функций. Для этого необходимо провести математическое преобразование, пользуясь соотношением 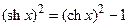 . В этом случае
. В этом случае 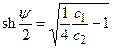 и уравнение (4.14) приобретает вид
и уравнение (4.14) приобретает вид 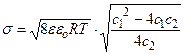 .
.
Рассмотренный метод определения σ известен как метод изоэффективных концентраций одно- и двухвалентных ионов.
Пример 4.6. Предположим, что в изолированных хлоропластах, помещенных в 0,01 М раствор KCl, расстояние между тилакоидными мембранами в гранах составляет h = 10 нм. Найти избыточную концентрацию ионов в зазоре между мембранами (по сравнению с концентрацией в среде) при условии, что отрицательный поверхностный заряд мембран σ составляет 20 мКл/м2.
Решение: В объеме между мембранами, несущими отрицательный фиксированный заряд, накапливается избыток свободных катионов, а анионы, напротив, исключаются из этого объема. Для того чтобы оценить содержание свободных катионов и анионов, необходимо знать величину электрического потенциала по центру расстояния между мембранами φ*. В промежутке между мембранами электрический потенциал меняется немонотонно по координате x, достигая минимума по абсолютной величине (φ*)по середине межмембранного зазора. Для одиночной мембраны в случае небольших потенциалов (приближение Дебая) абсолютная величина потенциала в двойном электрическом слое убывает экспоненциально с увеличением расстояния от границы: 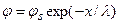 , где φs – поверхностный потенциал, а λ – длина экранирования, описываемая уравнением (4.13). В случае двух параллельно расположенных мембран распределение потенциала φ в зазоре включает две симметричные ветви и описывается суммой убывающей и нарастающей экспонент:
, где φs – поверхностный потенциал, а λ – длина экранирования, описываемая уравнением (4.13). В случае двух параллельно расположенных мембран распределение потенциала φ в зазоре включает две симметричные ветви и описывается суммой убывающей и нарастающей экспонент: 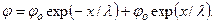 Из соображений симметрии за ноль координаты x удобно принять середину зазора между мембранами. В этой точке (при х = 0) потенциал минимален и составляет 2φо=φ*. На расстояниях х = ±h/2 значения потенциала равны потенциалу поверхности φs, т.е.
Из соображений симметрии за ноль координаты x удобно принять середину зазора между мембранами. В этой точке (при х = 0) потенциал минимален и составляет 2φо=φ*. На расстояниях х = ±h/2 значения потенциала равны потенциалу поверхности φs, т.е. 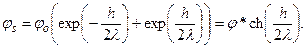 Условия задачи позволяют рассчитать длину экранирования по формуле (4.13), а также величину поверхностного потенциала φs по формуле (4.15). Избыточная концентрация ионов (К+ и Cl–) по центру межмембранного зазора по сравнению с концентрацией ионов в окружающей среде запишется в виде:
Условия задачи позволяют рассчитать длину экранирования по формуле (4.13), а также величину поверхностного потенциала φs по формуле (4.15). Избыточная концентрация ионов (К+ и Cl–) по центру межмембранного зазора по сравнению с концентрацией ионов в окружающей среде запишется в виде:
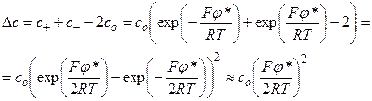
Длина экранирования для 0,01 М раствора KCl при T = 300 K равна по уравнению (4.13):
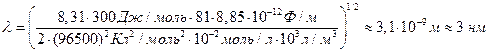 .
.
Поверхностный потенциал можно рассчитать по (4.15) или же воспользоваться равноценными представлениями о двойном слое как конденсаторе с зарядом на пластинах, равном σ, потенциалом φs и толщиной диэлектрического слоя λ. В последнем случае выполняется соотношение
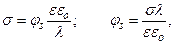 где
где 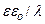 – емкость двойного электрического слоя.
– емкость двойного электрического слоя.
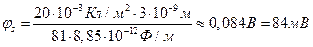 .
.
Потенциал φ* по центру между мембранами составит
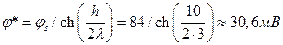 .
.
Избыточная концентрация осмотически активных частиц (ионов) по середине промежутка между мембранами составит
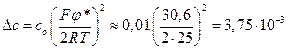 осмоль/л
осмоль/л
Следует отметить, что избыток ионов в промежутке между мембранами создает избыточное осмотическое давление, которое рассчитывают по уравнению Вант-Гоффа
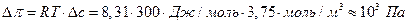 .
.
Дата добавления: 2015-06-22; просмотров: 2868;
