Диффузия в газах. Предположим, что в единице объёма двухкомпонентной газовой смеси содержится n1 молекул одного вида и n2 молекул другого вида

Предположим, что в единице объёма двухкомпонентной газовой смеси содержится n₁ молекул одного вида и n₂ молекул другого вида. Полное число молекул в единице объёма равно n = n₁ + n₂. Допустим, что в направлении оси х создаются градиенты концентраций 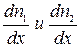, причём 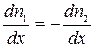. Однако вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах.

Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением

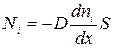где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Знак минус указывает на то, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i – го вида m_i, получим выражение для потока массы i – ой компоненты:

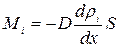где r_i = n_im_i – парциальная плотность i – ой компоненты.

Эти формулы представляют собой эмпирические уравнения диффузии. Их называют уравнением Фика.

для коэффициента диффузии выражение

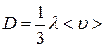Вязкость газов

Сила трения между двумя слоями жидкости может быть вычислена по формуле

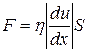где h- коэффициент вязкости, 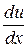- градиент скорости, т.е. величина, показывающая, как быстро изменяется скорость жидкости или газа в направлении х, перпендикулярном к направлению движения слоёв, S – величина поверхности, по которой действует сила F. Это уравнение и есть эмпирическое уравнение вязкости.

Согласно второму закону Ньютона, взаимодействие двух слоёв с силой F можно рассматривать как процесс, в ходе которого от одного слоя к другому передаётся в единицу времени импульс, по величине равный F. Поэтому уравнение вязкости можно представить в виде

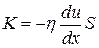где К- импульс, передаваемый за секунду от слоя к слою через поверхность S. Следовательно, величину К можно рассматривать как поток импульса через поверхность S. Знак минус в этой формуле обусловлен тем обстоятельством, что импульс “течёт” в направлении убывания скорости u.

выражение для коэффициента вязкости

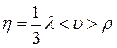ВЫВОД ПО ЧЕТВЕРТОМУ ВОПРОСУ:

Рассмотрели явления переноса: теплопроводность, диффузию и вязкость.

Коэффициенты, стоящие в законах описывающих явления переноса связаны между собой соотношениями:

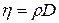
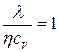
Основным объектом внимания термодинамики является термодинамическая система, т.е. любая совокупность физических тел. Состояние этой системы описывается с помощью ограниченного числа макроскопических величин или физических параметров. Например, для газа - это давление, объем, температура, масса и т.д. Для разных частей системы параметры могут принимать, вообще говоря, различные значения: так температуры в различных местах выбранного объема газа могут отличаться друг от друга. В этом случае говорят, что температура является неравновеснымпараметром. Если же параметры системы одинаковы для различных ее частей и сохраняются неизменными длительное время, то такое состояние системы называется равновесным.Строго говоря, термодинамика обязана рассматривать только равновесные состояния, т.к. в противном случае макроскопические значения параметров теряют свой смысл. В то же время термодинамику интересуют процессы передачи теплоты и совершение механической работы, т.е. для нее важны изменения в выбранной системе или переход из одного состояния в другое, т.е. процессы, протекающие в системе. Для удовлетворения этих противоречивых требований используется два приема: во-первых, любое изменение состояния рассматривается как квазиравновесное, т.е. состоящее из ряда последовательных равновесных состояний, причем параметры двух близких состояний отличаются друг от друга на бесконечно малую величину; во-вторых, термодинамика широко использует понятие функции состояния, т.к. знание самой функции и ее значения в некоторый начальный момент времени позволяют предсказать состояние системы в любой последующий момент времени безотносительно к условиям перехода из начального положения системы в конечное.

p I A · · B II V Рис. К определению процессов в термодинамической системе. (р-давление газа, V - его объем)

Будем рассматривать далее в качестве термодинамической системы один моль идеального газа. Процесс перехода из одного равновесного состояния в другое принято изображать графически (cм.рис.). Такой процесс называется равновесным. Кроме того, известно, что процесс в системе может быть обратимым и необратимым.Если процесс перехода системы из одного состояния в другое по пути I проходит через одни и те же промежуточные состояния в независимости от направления перехода, то такой процесс называется обратимым. Если же прямой и обратный переходы по пути I между состояниями А и

В происходят через различные промежуточные состояния, то такой переход необратим. Если переход из состояния А в В происходит по пути I , а обратный переход из В в А осуществляется по пути II, то такое изменение состояния системы называется циклом. Цикл также может быть обратимым или необратимым. Необратимым цикл будет всегда, если хотя бы одна часть его соответствует необратимому процессу.

Мы начинаем изучение термодинамики.

Вопрос № 5

Если два изолированных тела с разной температурой привести в контакт друг с другом, то через некоторое время их температуры выровняются, - наступит тепловое равновесие. Ясно, что при этом температура одного тела уменьшится, а другого увеличится. Это означает, что в месте теплового контакта молекулы одного тела при хаотическом движении передают свою энергию молекулам другого тела. Процесс передачи энергии путем хаотических микроскопических взаимодействий называется теплообменом (теплопередачей), а переданное при этом количество энергии - теплотой (теплом).

Внутренняя энергия идеального газа равна числу молекул газа, умноженному на среднюю кинетическую энергию одной молекулы.

U = N < e >

Среднюю энергию молекулы можно представить в виде:

< e > = < e_пост> + < e_вращ> + < e_колеб> .

При низких температурах ( Т < 1000К ) i = i_пост+ i_вращ .

Подсчитаем теперь внутреннюю энергию идеального газа:

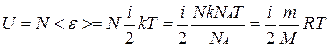где 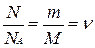- число молей газа (количество вещества), .

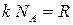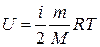- внутренняя энергия идеального газа

или в другой форме

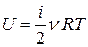Первое начало термодинамики:

Количество теплоты, сообщённое газу, идёт на приращение внутренней энергии газа и на совершение газом работы над внешними телами.

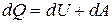- первое начало термодинамики.

Определим физические величины, входящие в этот закон.

а) Внутренняя энергия идеального газа равна

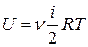где 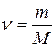- количество вещества, i – число степеней свободы молекул газа.

Тогда изменение внутренней энергии газа равно

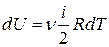- изменение внутренней энергии газа.

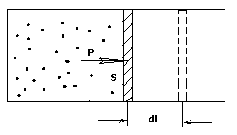Рис. 1

б) Вычислим теперь работу, совершаемую газом при изменении объёма. Для этого рассмотрим газ, находящийся в цилиндре под поршнем, который может свободно перемещаться. При нагревании давление газа P , будет оставаться постоянным, и, как видно из рисунка, работа, которую совершает газ, будет равна:

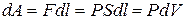где dV = S dl - изменение объема газа.

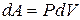- работа, совершаемая газом при изменении его объема

в) Наконец, найдём формулу для подсчёта количества теплоты, сообщенной газу массы 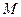при его нагревании на 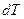. Для этого введем понятие молярной теплоёмкости газа

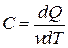Молярная теплоёмкость газа – это количество теплоты, сообщённой 1 молю газа, для увеличения его температуры на .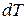

Тогда формула для подсчёта теплоты будет иметь вид

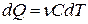- теплота, сообщённая газу для

увеличения его температуры на dT.

ВЫВОД ПО ПЯТОМУ ВОПРОСУ:

Вопрос № 6

Термодинамика изохорного процесса: V=const

Рассмотрим закон, описывающий этот процесс и его график в координатах (P,V). Этот закон является частным случаем уравнения состояния идеального газа:

рV = nRT.

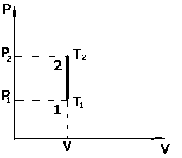
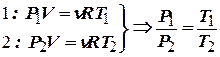. - закон Шарля.

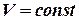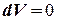Так как , то и 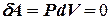, т.е. работа совершаемая газом при изохорнком процессе равна нулю.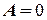

Тогда 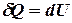- первое начало термодинамики для изохорного процесса.

Поскольку количество теплоты, сообщенное газу, равно

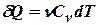где 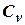- молярная теплоёмкость газа при постоянном объёме, то мы получаем полезную формулу для подсчёта приращения внутренней энергии газа:

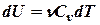- изменение внутренней энергии газа.

Сравнивая эту формулу с другой формулой

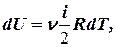
получим выражение для молярной теплоёмкости газа при постоянном объёме: .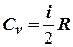

Подводимое к газу тепло затрачивается на изменение внутренней энергии газа. Работа расширения равна нулю.

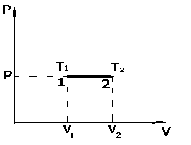
Термодинамика изобарного процесса: P=const.

Соотношение Майера

Сначала рассмотрим закон, описывающий этот процесс и его график в координатах (P,V).

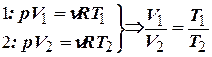- закон Гей-Люссака.

Теперь работа, совершаемая газом,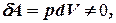

приращение внутренней энергии газа тоже не равно нулю 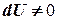, и первое начало термодинамики не меняет своего вида:

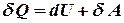первое начало термодинамики для изобарного процесса.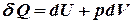

Обмен энергией при изобарическом процессе происходит в форме работы, и в форме теплопередачи. Подводимое к газу тепло затрачивается на изменение внутренней энергии газа и на совершение им работы.

Формула для подсчёта теплоты теперь примет вид

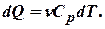
где 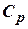- молярная теплоёмкость газа при постоянном давлении.

Приращение внутренней энергии запишем в виде

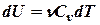
Работу, совершаемую газом, также представим в аналогичном виде

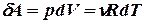Здесь мы воспользовались уравнением Менделеева-Клапейрона 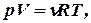дифференциальное уравнение которого при 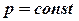дает

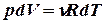Работа расширения газа при изобарном процессе

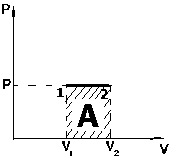
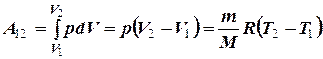
На графике (P,V) работа, совершаемая газом, численно равна площади прямоугольника, построенного под изобарой.

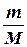=1 и 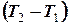=1, то 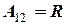, т.е. универсальная газовая постоянная численно равна работе, совершаемой одним молем идеального газа, при изобарическом нагревании его на один Кельвин.

Из выражения для работы следует размерность и физический смысл универсальной газовой постоянной R:

, .

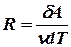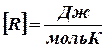Универсальная газовая постоянная R численно равно работе, совершённой одним молем газа при изобарическом процессе при увеличении его температуры на один градус.

Продолжим рассмотрение изобарного процесса. Подставляя полученные выражения для dQ, dU, dA в первое начало термодинамики, получим:

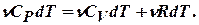
Сокращая на ndT, получим соотношение между молярными теплоёмкостями газа при постоянном объёме 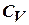и постоянном давлении :

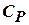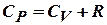- соотношение Майера.

Учитывая выражение для 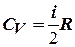, получим аналогичное выражение для : = .

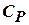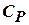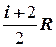Приведем также выражение для отношения молярных теплоёмкосте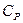й и : .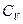

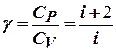Для двухатомных молекул при невысоких температурах i = 5, тогда 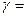1,4.

Термодинамика изотермического процесса: T=const.

Изотермический процесс – процесс, протекающий при постоянной температуре. Такой процесс возможен только при наличии идеального теплового контакта между газом и окружающей средой.

Приведем закон, описывающий этот процесс, и его график в координатах (P,V).

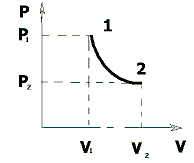
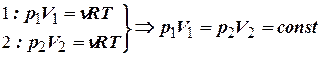– закон Бойля-Мариотта

Так как T = const, то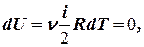

т. е. dU = 0 - изменение внутренней энергии газа при изотермическом процессе равно нулю.

Первое начало термодинамики для изотермического процесса .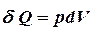

При изотермическом процессе газ обменивается энергией с внешней средой и в форме теплопередачи и в форме работы. Подводимое к газу тепло затрачивается только на совершение работы. Работа расширения газа при изотермическом расширении равна Q = A. Выпишем работу, совершаемую газом при изотермическом процессе. Используя уравнение Менделеева-Клапейрона 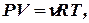представим элементарную работу в виде:

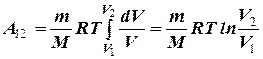
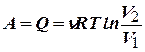–работа, совершаемая газом при изотермическом процессе

Учитывая то, что при изотермическом процессе 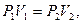работу можно вычислить также по формуле: ;

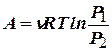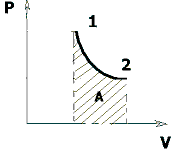
На графике (P,V) работа, совершаемая газом, численно равна площади под кривой, описывающий изотермический процесс.

ВЫВОД ПО ШЕСТОМУ ВОПРОСУ:

Применили первое начало термодинамики к изохорному, изобарному и изотермическому процессам.

Вопрос № 7.

Способность любого тела изменять свою температуру при сообщении ему теплоты характеризуется теплоемкостью тела.

Полная теплоемкость измеряется количеством теплоты, которое нужно сообщить системе, чтобы её температура изменилась на один градус.

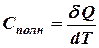. (9.7)

Молярная теплоемкость численно равна количеству тепла, которое необходимо сообщить одному молю вещества, чтобы повысить его температуру на единицу.

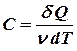(9.10)

Удельная теплоемкость численно равна количеству тепла, которое необходимо сообщить единице массы вещества, чтобы повысить его температуру на единицу.

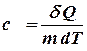(9.11)

Из формул следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение МКТ справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости, зависят от температуры.

Расхождение теории и эксперимента нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантовые энергии вращения и колебаний молекул. Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоемкость (соответствующая степень свободы "замораживается" – к ней неприменим закон равнораспределения энергии). Этим объясняется, что теплоемкость моля двухатомного газа – водорода – при комнатной температуре равна 5/2 R вместо 7/2 R. Аналогично можно объяснить уменьшение теплоемкости при низкой температуре ("замораживаются" вращательные степени свободы) и увеличение при высокой ("возбуждаются" колебательные степени свободы).

Адиабатический процесс-это процесс, протекающий без теплообмена с окружающей средой.

Поскольку δQ = 0, то первое начало термодинамики примет вид:

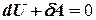- первое начало термодинамики при адиабатическом процессе

Такой вид первого начала термодинамики позволяет легко вычислить работу, совершаемую газом:

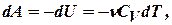
или для конечного адиабатического процесса:

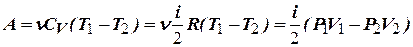- работа, совершаемая газом при адиабатическом процессе.

Вычислим работу, совершаемую газом в адиабатическом процессе.

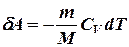
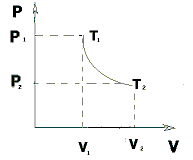
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшится от T₁ до T₂ и работа расширения равна

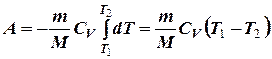
преобразуем уравнение к виду

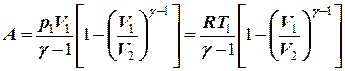
Работа, совершаемая при адиабатическом расширении 1-2, меньше чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

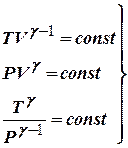- уравнения адиабаты.

Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости можно вывести уравнение политропы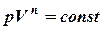

Где 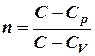– показатель политропы. Очевидно, что при

С=0, n=γ получается уравнение адиабаты;

С=∞, n=1 – уравнение изотермы

С=С_р, n=0 – уравнение изобары

С=С_V, n= 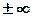– уравнение изохоры. Т.о. все рассмотренные процессы являются частными случаями политропного процесса.

Представим графики всех изопроцессов в одних и тех же координатных осях (P,V), причём пусть все они начинаются из одного и того же начального соединения 1.

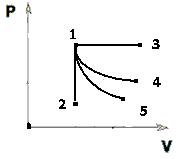
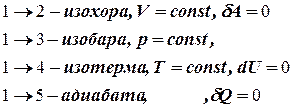
Сравним уравнения изотермы рV = const и адиабаты 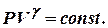Поскольку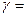 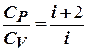> 1, то адиабата идёт круче изотермы, что видно с графиков изопроцессов.

ВЫВОД ПО СЕДЬМОМУ ВОПРОСУ:

Адиабатический процесс-это процесс, протекающий без теплообмена с окружающей средой.

Процесс, в котором теплоемкость остается постоянной, называетсяполитропным.

Вопрос № 8.

Равновесным состоянием системы называется такое состояние, при котором параметры системы имеют определённые значения, остающиеся при неизменных внешних условиях постоянными сколько угодно долго. Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновесным или квазистатическим. Из сказанного следует, что равновесным может быть только бесконечно медленный процесс. При достаточно медленном протекании реальные процессы могут приближаться к равновесному процессу сколько угодно близко. Равновесный процесс может быть проведен в обратном направлении, причём система будет проходит через те же состояния, что и при прямом ходе, но в обратной последовательности. Поэтому равновесные процессы называют также обратимыми процессами. В случае обратимого процесса при возвращении в исходное состояние ни в самой системе, ни в окружающих телах не остаётся никаких изменений. Если такие изменения появляются, то такой процесс называется необратимым процессом. Все реальные процессы необратимы. В механических процессах необратимость вызывается трением.

Энтропия 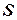– это такая функция состояния, дифференциал которой определяется отношением:

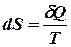В СИ энтропия 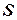измеряется в Дж/К.

Приведём формулы для подсчёта изменения энтропии в случае изопроцессов для идеального газа:

а) Изохорный процесс: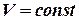

, .

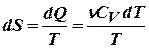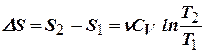б) Изобарный процесс: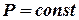

, .

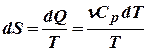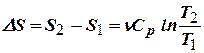в) Изотермический процесс: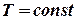

, .

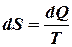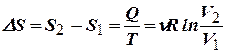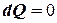
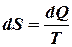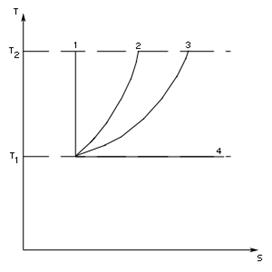
г) Адиабатический процесс:

, , .

- адиабатический процесс,

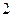- изохорический процесс,

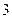- изобарический процесс,

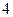- изотермический процесс.

Понятие энтропии имеет статистическое толкование. Состояние макроскопического тела (т.е. тела, образованного огромным количеством молекул) может быть задано с помощью объёма, давления, температуры, внутренней энергии и других макроскопических величин. Охарактеризованное таким способом состояние называется макросостоянием. Состояние макроскопического тела, охарактеризованное настолько подробно, что оказываются заданными состояния всех образующих тело молекул, называется микросостоянием. Всякое макросостояние может быть осуществлено различными способами, каждому из которых соответствует некоторое микросостояние тела. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом 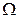или термодинамической вероятностью макросостояния. В статистической физике существует теорема, которая утверждает о равновероятности всех микросостояний данной системы. В качестве характеристики вероятности состояния можно было бы выбрать статистический вес 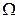, однако такая характеристика не обладала бы свойствами аддитивности. Поэтому в качестве характеристики состояния принимается величина S, пропорциональная логарифму статистического веса .

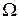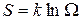, (4)

где 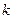- постоянная Больцмана. Такую величину называют энтропией.

Определённая таким образом энтропия обладает следующими свойствами:

1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная, т.е. предоставленная самой себе, система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины (4).

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

ВЫВОД ПО ВОСЬМОМУ ВОПРОСУ:

Энтропия 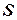– это такая функция состояния, дифференциал которой определяется отношением:

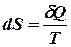Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом 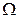или термодинамической вероятностью макросостояния.

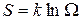
Вопрос № 9 .

Невозможно построить периодически действующую тепловую машину, которая бы всю подводимую к ней теплоту превращала в работу, т.е. всегда .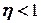

Повышение КПД тепловой машины является важнейшей практической задачей. Однако многочисленные попытки приблизиться к решению этой проблемы оказались безуспешными. Более того, английским ученым В. Томсоном (позднее лорд Кельвин) было сформулировано положение о невозможности построения такого двигателя, который был назван вечным двигателем второго рода. Это положение теперь называется вторым законом термодинамики. Полная формулировка этого закона в редакции Томсона гласит: невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.

Немецкий ученый Р. Клаузиус предложил другую формулировку этого закона: невозможен самопроизвольный переход тепла от холодного тела к горячему. Термин «самопроизвольный» означает, что такая передача теплоты должна происходить без каких-либо изменений в окружающих телах.

Однако многочисленные попытки приблизиться к решению этой проблемы оказались безуспешными. Более того, английским ученым В. Томсоном (позднее лорд Кельвин) было сформулировано положение о невозможности построения такого двигателя, который был назван вечным двигателем второго рода. Это положение теперь называется вторым законом термодинамики. Полная формулировка этого закона в редакции Томсона гласит: невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.

Энтропия изолированной системы может только возрастать, (либо по достижении максимального значения оставаться неизменной), т.е. .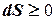

Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е. 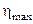. Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.

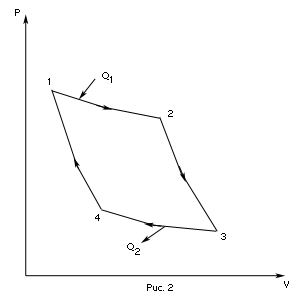Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты 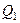равно работе 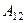, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна

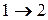- изотермическое расширение при ,

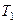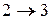- адиабатическое расширение, ,

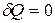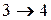- изотермическое сжатие при ,

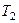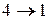- изотермическое сжатие, .

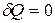КПД цикла Карно:

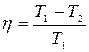где 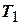- температура нагревателя, 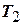- температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах 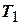и .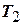

ВЫВОД ПО ДЕВЯТОМУ ВОПРОСУ:

Повышение КПД тепловой машины является важнейшей практической задачей.

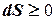Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е. 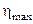. Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах 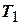и .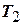

Вопрос № 10

Поведение реальных газов хорошо описывается в модели идеального газа, когда расстояния между молекулами очень велики по сравнению с размерами самих молекул.

Однако при больших степенях сжатия и при низких температурах становятся заметными отклонения в их поведении от уравнения Менделеева - Клапейрона. Причины такого отклонения достаточно банальны. Они связаны прежде всего с тем, что молекулы газа имеют конечный объем, тогда как в модели идеального газа они считаются материальными точками. Кроме того, между отдельными молекулами существуют силы взаимодействия, т.е. у молекул кроме кинетической энергии их хаотического движения появляется потенциальная энергия.

Голландский ученый Ван-дер-Ваальс первый сумел придумать новую модель, которая учитывала бы оба этих фактора. Он предположил, что между молекулами действуют силы притяжения, которые по своей природе являются электрическими.

Каждую молекулу он рассматривал как твердый шар некоторого диаметра d. В этом случае ясно, что молекулы не могут подойти друг к другу ближе этого расстояния. В теории строения кристаллов показывается, что N таких шаров при условии тесного соприкосновения друг с другом занимают объем в четыре раза больший, чем 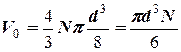, т. е. пустоты между шарами имеют объем в три раза больший, чем объем самих шаров. Поэтому величину объема газа V, входящего в уравнение Менделеева - Клапейрона, надо заменить на новую величину (V-b), где b рассматривается как некоторая поправка на истинный объем, доступный молекулам газа. Далее он учел, что молекулы могут взаимодействовать не только друг с другом, но и с окружающими их стенками сосуда. Если силы взаимодействия между молекулами (см. рис.) вдали от стенки в энергию молекулы при ее ударе об стенку. Величина работы этой силы зависит от количества молекул в сфере эффективного взаимодействия, т.е. от концентрации молекул в сосуде - n.

p_i = 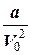, где а - некий новый коэффициент пропорциональности, зависящий от природы молекул и количества газа.

Подставляя выражение для р_i и учитывая поправку на конечный объем молекул (объем V₀ необходимо заменить новой величиной (V₀ - b)), приходим к новому уравнению состояния, описывающего свойства реальных газов:

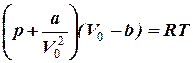
называемому уравнением Ван-дер-Ваальса.

Для произвольной массы газа

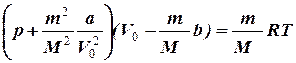
ВЫВОД ПО ДЕСЯТОМУ ВОПРОСУ:

В отличие от идеального газа, молекулы реального газа имеют собственный объем и взаимодействуют между собой. Голландский ученый Ван-дер-Ваальс первый сумел придумать новую модель, которая учитывала бы оба этих фактора. С учетом поправок, уравнение состояние имеет вид

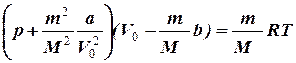Вопрос № 11.

Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм.

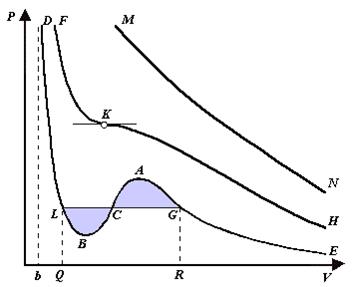
При более низких температурах и надлежащих значениях давления Р уравнение (6) имеет три корня V₁, V₂, V₃ . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается. При некоторой промежуточной температуре три корня V₁, V₂, V₃ становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление P_k , объем V_k и температура T_k называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим.

Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. Для этого необходимо еще, чтобы они были термодинамически устойчивы. Одно из необходимых условий термодинамической устойчивости физически однородного вещества состоит в выполнении неравенства 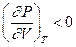. Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены.

При специальных условиях могут быть реализованы состояния, изображаемые участками изотермы GA и BL. Эти состояния называются метастабильными. Участок GA изображает так называемый пересыщенный пар, участок BL - перегретую жидкость. Обе фазы обладают ограниченной устойчивостью. Каждая из них может существовать до тех пор, пока она не граничит с другой более устойчивой фазой. Например, пересыщенный пар переходит в насыщенный, если в него ввести капли жидкости. Перегретая жидкость закипает, если в нее попадают пузырьки воздуха или пара.

ВЫВОД ПО ОДИННАДЦАТОМУ ВОПРОСУ:

Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. При специальных условиях могут быть реализованы метастабильные состояния.

Вопрос № 12

В жидких и твердых телах при любой температуре имеется некоторое количество молекул, энергия которых оказывается достаточной для того, чтобы преодолеть притяжение к другим молекулам, покинуть поверхность жидкости или твердого тела и перейти в газообразную фазу. Переход жидкости в газообразную фазу называется испарением, переход в газообразное состояние твердого тела носит название сублимации.

Все твердые тела без исключения в той или иной степени сублимируют. У одних веществ, таких, например, как углекислота, процесс сублимации протекает с заметной скоростью; у других веществ этот процесс при обычных температурах столь незначителен, что практически не обнаруживается.

При испарении и сублимации тело покидают наиболее быстрые молекулы, вследствие чего средняя энергия оставшихся молекул уменьшается и тело охлаждается. Чтобы поддерживать температуру испаряющегося (или сублимирующегося) тела неизменной, к нему нужно непрерывно подводить теплоту. Количество теплоты q, которое необходимо сообщить единице массы вещества для того, чтобы превратить ее в пар, находящийся при той температуре, которую имело вещество до испарения, называется удельной теплотой испарения (или сублимации).

При конденсации теплота, затрачиваемая при испарении, Отдается обратно: образующаяся при конденсации жидкость (или твердое тело) нагревается.

Рассмотрим процесс установления равновесия между жидкостью и ее паром. Возьмем герметичный сосуд, частично заполненный жидкостью, и допустим, что первоначально из пространства над жидкостью вещество полностью удалено. Вследствие процесса испарения пространство над жидкостью будет наполняться молекулами. Молекулы, перешедшие в газообразную фазу, двигаясь хаотически, ударяются о поверхность жидкости, причем часть таких ударом будет сопровождаться переходом молекул в жидкую фазу. Число молекул, переходящих в единицу времени в жидкую фазу, пропорционально числу ударяющихся о поверхность молекул, которое в свою очередь пропорционально 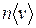, т.е. растет с давлением. Следовательно, наряду с испарением протекает обратный процесс перехода молекул из газообразной в жидкую фазу, причем интенсивность его растет по мере увеличения плотности молекул в пространстве над жидкостью. При достижении некоторого, определенного давления количества молекул, покидающих жидкость и возвращающихся в нее, станут равны. Начиная с этого момента плотность пара перестает изменяться. Между жидкостью и паром устанавливается подвижное равновесие, которое будет существовать до тех пор, пока не изменится объем или температура системы. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Давление, при котором наблюдается равновесие, называется давлением (упругостью) насыщенного пара.

Число молекул, покидающих жидкость в единицу времени, сильно растет с температурой. Число молекул, ударяющихся о поверхность жидкости, зависит от температуры в меньшей степени (через 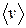как 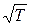). Поэтому при повышении температуры равновесие между фазами нарушается, и в течение некоторого времени поток молекул в направлении жидкость →пар будет превышать поток в направлении пар→жидкость. Это продолжается до тех пор, пока возрастание давления не приведет снова к установлению подвижного равновесия. Т.о., давление, при котором устанавливается подвижное равновесие между жидкостью и паром, т.е. давление насыщенных паров, оказывается зависим от температуры.

Если увеличить объем сосуда, то давление пара упадет, и равновесие будет нарушено. в результате в пар превратится дополнительное количество жидкости, такое, чтобы давление пара стало вновь равным р _н.п.

123 4

Дата добавления: 2015-06-17; просмотров: 1513;