позволяет определить наклоны кривых равновесия.

Здесь L — теплота фазового перехода (например, в случае плавления — удельная теплота плавления), (V₂—V_l) — изменение объема вещества при переходе его из первой фазы во вторую, Т — температура перехода (например, в случае плавления — температура плавления Т_пл).

Поскольку L и Т всегда положительны, то наклон кривой равновесия определяется знаком (V₂ — V₁). Так при испарении и сублимации объем всегда возрастает, поэтому dp/dT > 0.

При плавлении у большинства веществ объем возрастает, следовательно dp/dT >0, т.е. увеличение давления приводит к повышению температуры плавления (сплошная КП на рисунке).

Для некоторых веществ (вода, Ge, чугун) объем жидкой фазы меньше объема твердой фазы, т.е. dp/dT < 0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рисунке).

Анализ диаграммы состояния

Диаграмма состояния, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить в том или ином процессе.

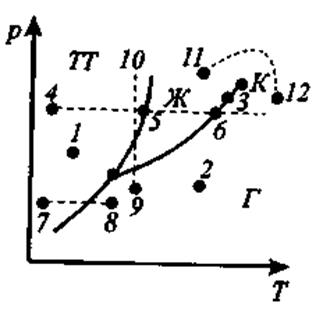
Например, при условиях, обозначенных: точкой 1 вещество — в твердом состоянии (ТТ), 2— в газообразном (Г), 3— одновременно в жидком (Ж)и газообразном.

При изобарном нагреве 4-5-6 в точке 5 начинается плавление, 6— кипение.

При изобарном нагреве 7-8 твердое тело превращается в газ, минуя жидкую фазу.

При изотермическом сжатии 9-10 вещество пройдет три состояния: газ-жидкость-кристалл.

Кривая испарения заканчивается критической точкой (К). Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11-12), т.е. такой переход, который не сопровождается фазовыми превращениями.

Это возможно потому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными).

Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р = 0 и Т = 0.

ВЫВОД ПО ТРИНАДЦАТОМУ ВОПРОСУ:

Для наглядного изображения фазовых превращений используется диаграмма состояния, на которой в координатах (р, Т)задается зависимость между температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), разделяющих поле диаграммы на три области, соответствующие условиям существования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз.

Диаграмма состояния, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить в том или ином процессе.

ВЫВОД ПО ЗАНЯТИЮ:

Все вещества состоят из мельчайших частиц - атомов и молекул.

Молекулы и атомы любого вещества находятся в непрерывном хаотическом движении, которое называется тепловым движением. При нагревании вещества интенсивность движения частиц увеличивается.

Молекулы вещества взаимодействуют между собой с силами притяжения F_пр и отталкивания F_от.

Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы. Обычно в качестве термодинамических параметров выбирают давление P, объем V и температуру T.

Соотношение, устанавливающее связь между параметрами состояния системы называется уравнением состояния термодинамической системы. Если какой либо из термодинамических параметров системы изменяется, то происходит изменение состояния системы, называемое термодинамическим процессом.

Уравнение Менделеева-Клапейрона – уравнение состояния идеального газа.

Все тела состоят из огромного числа частиц, движение которых хаотично и сопровождается массовыми столкновениями. Тем не менее в таком хаотическом движении устанавливаются стабильные закономерности статического характера.

Между телами возникают явления переноса: теплопроводность, диффузию и вязкость.

Рассмотрели первое и второе начало термодинамики, физический смысл внутренней энергии, теплоемкости, энтропии.

В отличие от идеального газа, молекулы реального газа имеют собственный объем и взаимодействуют между собой. Голландский ученый Ван-дер-Ваальс первый сумел придумать новую модель, которая учитывала бы оба этих фактора.

Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. При специальных условиях могут быть реализованы метастабильные состояния.

В жидких и твердых телах при любой температуре имеется некоторое количество молекул, энергия которых оказывается достаточной для того, чтобы преодолеть притяжение к другим молекулам, покинуть поверхность жидкости или твердого тела и перейти в газообразную фазу. Переход жидкости в газообразную фазу называется испарением, переход в газообразное состояние твердого тела носит название сублимации.

Диаграмма состояния, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить в том или ином процессе.

14.Заключение).

Молекулярная физика и термодинамика — разделы физики, в которых изучаются зависимости свойств тел от их строения, взаимодействия между частицами, из которых состоят тела, и характера движения частиц.

Для исследования физических свойств макроскопических систем, связанных с огромным числом содержащихся в них атомов и молекул, применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (или молекулярно-кинетический) и термодинамический.

Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему.

Этот метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении.

Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц.

Этот метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия.

При рассмотрении реальных газов необходимо учитывать собственный объем молекул и силы межмолекулярного взаимодействия.

Силы межмолекулярного взаимодействия — короткодействующие — они проявляются на расстояниях менее 10^–9 м. Сила взаимодействия молекул — это равнодействующая сил притяжения F_n (они преобладают на больших расстояниях) и сил отталкивания F_o (они доминируют на малых расстояниях). На расстоянии r = r₀ эти силы уравновешивают друг друга и F = 0. Таким образом, расстояние r₀ —это равновесное расстояние между молекулами, на котором бы они находились в отсутствие теплового движения.

Потенциальная энергия взаимодействия молекул U минимальна в состоянии устойчивого равновесия при r = r₀.

Соотношение между U_min и kТ является критерием различных агрегатных состояний. U_min определяет работу, которую нужно совершить против сил притяжения, чтобы разъединить молекулы, находящиеся в равновесии (r = r₀). kТ определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы теплового движения молекул.

При U_min << kТ вещество находится в газообразном состоянии, т.к. тепловое движение молекул препятствует соединению (конденсации) молекул.

При U_min >> kТ вещество находится в твердом состоянии, т.к. тепловой энергии недостаточно, чтобы "оторвать" молекулы друг от друга.

При U_min ≈ kТ вещество находится в жидком состоянии, т.к. в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояния, превышающие r₀.

К следующему занятию слушатели должны:

- знать:

понятия термодинамической системы, параметров состояния термодинамической системы, термодинамического процесса, основное уравнение состояния термодинамической системы, физический смысл параметров состояния, виды процессов; понятия средней, среднеквадратичной и наивероятнейшей скорости молекул, вид распределения Максвелла по скоростям и энергиям, распределение Больцмана, барометрическую формулу, виды явлений переноса, понятия внутренней энергии, степени свободы, теплоемкости идеального газа, первое начало термодинамики, уравнение Майера; понятия обратимого и необратимого процесса, термодинамического цикла, энтропии, второе начало термодинамики, понятия реального газа, уравнение Ван-дер-Ваальса, физический смысл констант Ван-дер-Ваальса; суть процессов испарения, конденсации, плавления и кристаллизации, понятие тройной точки, уравнение Клапейрона–Клаузиуса, виды кристаллических решеток, закон Дюлонга и Пти.

- уметь:

определять параметры состояния термодинамической системы, различать по графику изопроцессы; определять среднюю, среднеквадратичную и наивероятнейшую скорости молекул, параметры, характеризующие явления переноса, применять первое начало термодинамики для анализа изопроцессов; определять изменение энтропии в различных процессах, исследовать термодинамические циклы, определять критические параметры газа Ван-дер-Ваальса, анализировать изотермы Ван-дер-Ваальса; анализировать диаграммы состояния.

- иметь представление:

о статистическом и термодинамическом методах исследования; о роли явлений переноса при развитии пожара, об адиабатном и политропно процессах;о работе тепловых двигателей и холодильных машин, о различиях реального и идеального газа, эффекте Джоуля-Томсона; об учете фазовых превращений при тушении пожаров.