Геоэлектрический разрез, эквивалентность кривых ВЭЗ.стр162-163, 190

В реальных геологических разрезах электромагнитные свойства горных пород весьма быстро изменяются с глубиной. Такое изменение обусловлено многими факторами: условиями осадконакопления, температурным и гидродинамическим режимами, давлением и т.п. Однако нередко в определенных интервалах глубин электромагнитные свойства горных пород оказываются примерно постоянным. В этом случае геологический разрез можно представить в виде отдельных слоев, в каждом из которых электромагнитные свойства, удельное электрическое, сопротивление, диэлектрическая и магнитная проницаемость – постоянны. Т.о., под геоэлектрическим разрезом понимают совокупность отдельных слоев конечной мощности с постоянными внутри каждого слоя электромагнитными параметрами. Такой разрез является только некоторой физической моделью реального геологического разреза. Если в геоэлектрическом разрезе имеется достаточно мощный слой с аномально высоким или аномально низким значениями электромагнитных параметров, то такой слой называется опорным геоэлектрическим горизонтом.

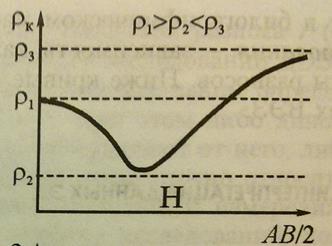
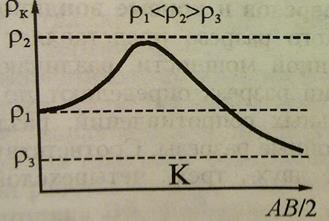
Совпадение кривых ВЭЗ для различных слоистых разрезов называется эквивалентностью кривых. Один из случаев проявления эквивалентности кривых ВЭЗ -это случай многослойного разреза: когда при относительно малых мощностях промежуточных пластов форма кривой определяется не удельным сопротивлением и мощностью каждого промежуточного слоя, а их продольной проводимостью. Эквивалентность кривых ВЭЗ необходимо учитывать при интерпретации полевых материалов.

На примере трехслойных кривых ВЭЗ можно показать, что их форма для разрезов p1> p2< p3 при небольшой мощности второго слоя определяется его проводимостью h2/ p2.

При p1< p2> p3 кривые будут эквивалентны. Эквивалентность кривых учитывают при интерпретации полевых материалов.

9. Интерпретация данных ВЭЗстр197-198 Качественная. Выполняют с целью получения общих представлений о структурных особенностях изучаемого района: обнаружения зон выклиивания горизонта, трассирование тектонических нарушений.

1. Карта типов кривых ВЭЗ. Тип кривой ВЭЗ определяется геоэлектрическим разрезом

2. Карта изолиний продольной проводимости. Если по кривым ВЭЗ определена продольная проводимость над опорной толщей то можно построить карту. Эта карта при условии постоянства плотности отражает глубину залегания опорного горизонта на площади исследования: большим значением продольной проводимости соответсвуют точки глубокого залегания опорного горизонта и наоборот. (график). Отрезок отсекаемого асимптотой на оси абцис. Численно равно продольной проводимости пачки двух слоев. Этот случай когда проводящая осадочная порода залегает на не проводящем основании( соленные отложения породы кристаллического фундамента).

3.Карта равных значений кажущегося сопротвления. Карта изоом. На кривых ВЭЗ определяют значения р₀ кажущего при постоянном разносе. Качественно отражает изменение глубины залегания опорного эл. горизонта на площади исследований.

Колличественная. Состоит в определении мощности и удельного сопротивления слоев геологического разреза. Интерпретацию проводят в предположении горизонтально-слоистой изучаемой среды, для которой рассчитано теоретически кривые ВЭЗ. Первый подход палетки. Второй: обратная задача решается с прямой. При количественной интерпретации решают обратную задачу – из кривых ВЭЗ получают удельные сопротивления и мощности слоев. Существуют два способа: палеточный и компьютерный.

В компьютерном способе используется подбор к наблюденной кривой ВЭЗ теоретической. В случае их совпадения считается, что параметры теоретической кривой соответствуют параметрам изучаемого геоэлектрического разреза. Решение прямой задачи производится в процессе интерпретации. Палеточный способ состоит в решении обратной задачи по наборам заранее рассчитанных кривых ВЭЗ для горизонтально слоистой среды с ограниченным числом слоев.

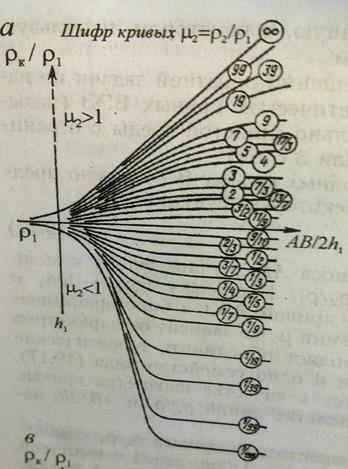
На рисунке асимптотами кривых pк/p1 являются: при АВ/2h1→0 значение pк/p1=1, т.е левой асимптотой является ось абсцисс; при АВ/2h1→∞ значение pк/p1= p2/p1, т.е правые асимптоты – горизонтальные линии, отсекающие на оси ординат отрезки p2/p1. μ2= p2/p1→∞, в том случае если первая асимптота имеет наклон 45˚относительно оси абсцисс.