Представление кривых и работа с ними

Для каждого криволинейного ребра в компьютере хранится либо уравнение кри­вой, либо эквивалентные характеристические параметры. Эти сведения важны как для систем автоматизированной разработки чертежей, так и для систем объемного моделирования. Эта процедура выполняется при создании и модифицировании кривых в системах автоматизированной разработки чертежей и системах поверхностного моделирования. Рассмотрим различные методы представле­ния уравнений кривых и методы работы с ними.

Уравнения кривых могут быть разделены на два основных типа. К первому типу относятся параметрические уравнения, описывающие связь координат х, у и z точки кривой с параметром. Ко второму типу относятся непараметрические уравнения, связывающие координаты х, у и zнекоторой функцией. Проще всего продемонстрировать различие между ними на примере. Рассмотрим окружность радиуса R, расположенную в начале системы координат. Если окружность лежит в плоскости ху, ее параметрическое уравнение может быть, например, таким:

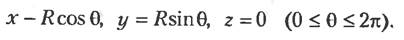
Центр, радиус и вектор нормали к плоскости, в которой лежит окружность, — примеры характеристических параметров, эквивалентных уравнению окружности.

Ту же окружность можно описать уравнением и без параметра:

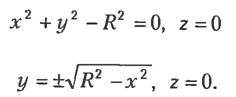
У каждого типа уравнений, примеры которых приведены выше, есть свои пре­имущества и недостатки, определяющие удобство их применения для различных целей. Мы сосредоточим внимание на применении уравнений к отображению кривых, поскольку интерактивная графика является одной из важнейших функ­ций САПР. Кривая, отображаемая на экране, в действительности представляет собой набор коротких отрезков. Поэтому постоянно возникает необходимость вычислять координаты точек кривой, находящихся на равном расстоянии друг от друга. Это называется вычислением кривой (cuive evaluation). Можно ожидать, что точки окружности, заданной уравнением, могут быть получены подста­новкой последовательных значений параметра, отличающихся друг от друга на небольшую величину.

Эллипс, как и окружность, может быть задан параметрическим уравнением. За­пишем такое уравнение для эллипса, лежащего в плоскости ху, с центром в начале координат. Положим, что большая ось эллипса направлена вдоль оси х и имеет длину а, а малая ось направлена вдоль оси уи имеет длину b. Параметрическое уравнение эллипса будет таким:

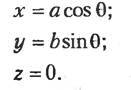
Диапазон значений параметра для эллипса составляет [0, 2p], а для дуги эллипса может быть более узким. Произвольный эллипс на произвольной плоскости с произвольными направлениями большой и малой осей получается в результате применения матриц преобразования, подобно тому, как мы делали это с окруж­ностью.

Чаще всего для описания кривых, используемых в программах CAD, использу­ются уравнения третьего порядка, потому что они обладают важным свойством: две кривые, описываемые такими уравнениями, могут быть соединены таким образом, что вторые производные в точке соединения будут равны друг другу. Это означает, что кривизна в точке соединения остается постоянной, отчего две кривые кажутся одним целым. Ту же непрерывность можно получить и для кри­вых более высоких порядков, однако работа с ними требует интенсивных вычис­лений.

В начале 60-х гг. Безье — сотрудник французской автомобильной компании «Рено» — предложил новую форму уравнения кривой и использовал ее в систе­ме поверхностного моделирования . Эта кривая получила назва­ние кривой Безье (Bezier curve). Она строится по вершинам многоугольника, за­ключающего ее в себе. Вершины сопрягаются соответствующими функциями подобно тому, как это делается при построении эрмитовой кривой. Безье выбрал функции сопряжения таким образом, чтобы получающаяся кривая удовлетворя­ла следующим требованиям.

- Кривая проходит через первую и последнюю вершины многоугольника.

- Направление вектора касательной в первой точке кривой совпадает с направ­лением первого отрезка многоугольника. Аналогичным образом, по­следний отрезок многоугольника определяет направление касательной в ко­нечной точке кривой.

- Производная степени n в начальной (или конечной) точке кривой определя­ется положением первых (или последних) n + 1 вершин многоугольника. Это свойство очень удобно при соединении двух кривых Безье, если требуется удовлетворить требованию непрерывности высших производных в точке со­единения. Вообще говоря, второе свойство есть частный случай данного свой­ства.

При изменении порядка вершин многоугольника на противоположный полу­чается та же самая кривая.

Задавшись этими требованиями, Безье выбрал в качестве функций сопряжения полином Бернштейна:

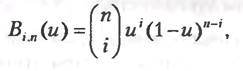(1)

где

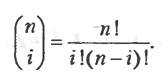
Если функцию сопряжения (1) применить к вершинам многоугольника, по­лучается уравнение кривой Безье:

(2)

где Р, — радиус-вектор n-й вершины. Вершины многоугольника называются за­дающими (control vertices), как и сам многоугольник (control polygon). Из форму­лы (2) видно, что для кривой, заданной n + 1 точками, максимальная степень будет 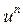. Таким образом, степень кривой Безье определяется количеством задаю­щих точек. Кривые Безье разных степеней с разным количеством задающих то­чек показаны на рис. 4.1

Рис. 4.1. Кривые Безье различных степеней

Даже если у нас есть формула, описывающая кривую, например уравнение кри­вой Безье, это уравнение будет практически бесполезным, если мы не найдем эффективного способа вычислять координаты точек на кривой. Мы знаем, что для отображения кривой необходимо вычислять координаты точек с небольшим приращением параметра, и делать это достаточно эффективно. Посмотрев на уравнение кривой Безье (1), можно прийти к выводу, что нам придется доста­точно часто вычислять биномиальный коэффициент

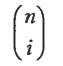
в функции сопряжения, а это требует серьезных затрат. Поэтому нужен алгоритм, позволяющий вычислить точку на кривой Безье не­посредственно, без вычисления значений биномиальных коэффициентов. Такой алгоритм существует и называется алгоритмом де Кастилъо.