Адиабатические процессы в газах.

Говорят, что термодинамическая система совершает адиабатический процесс, если он обратим и если система термически изолирована, так что во время процесса не происходит теплообмен между системой и окружающей средой.

Если дать возможность газу адиабатически расширяться, то он произведёт работу и её величина будет положительной.

Так как газ термически изолирован ( Q = 0), то значение ∆U должно быть отрицательным, т.е. во время адиабатического расширения внутренняя энергия газа уменьшается.

Из уравнения (I, 40) следует:

PdV + C_VdT = 0 (I, 42)

Выразив давление из (I, 36) и разделив на T, получим

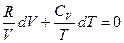
Полагая C_V независимым от T и интегрируя, получаем:

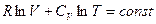
Из (I, 38) следует, что 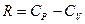. Подставляя это выражение для R и деля на C_V получаем:

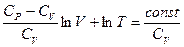
Если ввести обозначение 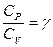, то после потенцирования получим уравнение адиабаты:

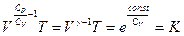, (I, 43)

где K и 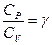- постоянные.

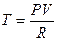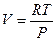Подстановка и приводит к двум другим возможным формам уравнения адиабаты:

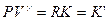(I, 44)

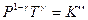(I, 45)

Уравнения (I, 43), (I, 44) и (I, 45) являются термодинамическими уравнениями , т.к. они вытекают из первого закона термодинамики и уравнения состояния идеального газа, поэтому приложимы лишь к идеальным газам и не являются общими уравнениями, справедливыми для любых систем.

Уравнение (I, 44) следует сравнить с уравнением изотермы для идеального газа:

PV = const

На диаграмме P – V изотермы являются семейством равнобочных гипербол. Адиабата по сравнению с гиперболой круче, т.к. показатель степени g больше единицы.

Интересным и простым приложением теории адиабатического расширения газов является вычисление изменения температуры при удалении от земной поверхности. Основной причиной изменения температуры являются конвекционные токи в тропосфере, которые непрерывно перемещают воздух из нижних слоёв в более высокие слои и наоборот. Когда воздух с уровня моря поднимается в верхние слои с низким давлением, он расширяется. Т.к. воздух – плохой проводник тепла, то теплота от окружающего воздуха очень мало передаётся новым подвижным слоям, поэтому можно считать, что происходит адиабатическое расширение. Соответственно понижается температура поднявшегося воздуха. С другой стороны, воздух верхних слоёв атмосферы, опускаясь вниз, испытывает адиабатическое сжатие, вследствие чего повышается температура.

Чтобы рассчитать изменение температуры, рассмотрим столб воздуха с единичным сечением. Гидростатическое давление столба воздуха высотой dH равно 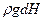, где g – ускорение свободного падения, а r - плотность воздуха.

Следовательно, при подъёме на расстояние dH давление уменьшится на величину .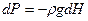

Из уравнения Менделеева-Клапейрона 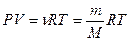получаем:

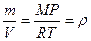, где m – масса и М – молекулярная масса газа. Тогда

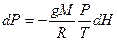(I, 46)

После логарифмирования и дифференцирования уравнения (I, 45) получаем:

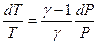(I, 47)

Подставляя в (I, 47) значение dP из (I, 46), получаем:

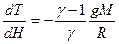
Полагая R = 8,314 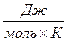, g = 9,81 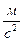, M = 0,0289 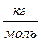и

g = 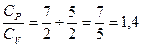(газы земной атмосферы двухатомны, ничтожными количествами одноатомных инертных газов можно пренебречь), получим:

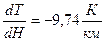
В действительности эта величина несколько больше, чем наблюдаемое среднее снижение температуры в зависимости от высоты над уровнем моря. Разница объясняется главным образом тем, что мы пренебрегли эффектом конденсации водяного пара в расширяющихся массах воздуха.