Химическая переменная. Формулировка первого закона термодинамики для процессов, сопровождающихся химическими и фазовыми превращениями.
Уравнения (I,25), (I, 25а) и ранее приведённые формулировки первого закона термодинамики справедливы для любой равновесной закрытой системы вне зависимости от того, происходят в ней химические или фазовые превращения или нет. Но при этом переменные, выражающие состав системы, не входили в набор независимых переменных, определяющих изменения Q, U и H. Пользуясь этими уравнениями, нельзя отделить влияние состава системы на её свойства от влияния независимых переменных Р и Т или V и T, что является недостатком термодинамической модели, скрывающим характерные особенности систем с изменяющимся химическим или фазовым составом.
Например, при атмосферном давлении и 298 К газообразный диоксид азота NO2 имеет мольную теплоёмкость 37 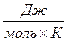 , а его димер N2O4 - 77
, а его димер N2O4 - 77 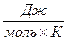 , в то же время экспериментально измеренная теплоёмкость равновесной смеси NO2 и N2O4 при тех же условиях составляет 518
, в то же время экспериментально измеренная теплоёмкость равновесной смеси NO2 и N2O4 при тех же условиях составляет 518 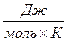 . Следовательно, теплота при нагревании смеси в основном затрачивается на диссоциацию димера, а не на непосредственное нагревание составляющих смесь веществ.
. Следовательно, теплота при нагревании смеси в основном затрачивается на диссоциацию димера, а не на непосредственное нагревание составляющих смесь веществ.
Чтобы устранить отмеченный недостаток, применяется следующий характерный для химической термодинамики приём – расширение набора переменных. Вместо функции 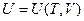 , использованной при выводе (I,26), для равновесной закрытой системы записывают:
, использованной при выводе (I,26), для равновесной закрытой системы записывают: 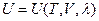 , где l - химическая переменная. Остановимся подробнее на этом понятии.
, где l - химическая переменная. Остановимся подробнее на этом понятии.
Химические реакции обратимы: наряду с химическим взаимодействием между исходными веществами (прямая реакция) протекает химическое взаимодействие между продуктами реакции (обратная реакция), в результате которого снова образуются исходные вещества. По мере протекания процесса скорость прямой реакции (число молекул продуктов реакции, образующихся в единицу времени) уменьшается, а скорость обратной реакции увеличивается. Когда обе скорости сравниваются, наступает состояние химического равновесия. Это означает, что число молекул всех веществ, образующих данную систему, не изменяется во времени при неизменных внешних условиях. Химическое равновесие является динамичным и подвижным – с изменением внешних условий равновесие сдвигается в ту или другую сторону и возвращается в исходное состояние, если внешние условия принимают первоначальные значения. Бесконечно малое изменение внешних условий влечёт за собой бесконечно малое изменение состояния равновесия.
Рассмотрим в общем виде газофазную реакцию:

Обозначим изменение количеств реагирующих веществ (в моль) в процессе реакции через 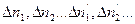 При этом количества исходных веществ будут уменьшаться, а количества продуктов реакции - увеличиваться. В этом случае следовало бы представить внутреннюю энергию как функцию параметров системы и числа молей каждого из участников реакции
При этом количества исходных веществ будут уменьшаться, а количества продуктов реакции - увеличиваться. В этом случае следовало бы представить внутреннюю энергию как функцию параметров системы и числа молей каждого из участников реакции 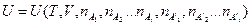
Однако, следует принять во внимание, что изменение количеств реагирующих веществ будут связаны между собой следующим соотношением:
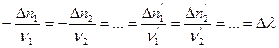 (I,54) или
(I,54) или

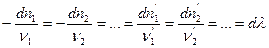 (I, 55)
(I, 55)
Отношение изменения числа молей всех участников реакции к соответствующим стехиометрическим коэффициентам одинаково и равно Dl. Эту величину, называемую химической переменной (число пробегов реакции, степень полноты реакции, степень превращения), принимают равной нулю в момент смешения реагентов (начало реакции) и равной единице, если число молей прореагировавших веществ равно соответствующим стехиометрических коэффициентам, т.е. когда 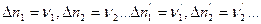
Таким образом, изменение химической переменной Dl в пределах одного пробега реакции может принимать значения от 0 до1 и характеризует полноту протекания реакции.
Например, если при синтезе аммиака по уравнению: 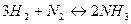 к моменту установления равновесия прореагируют 3 моль водорода и 1 моль азота, то Dl =1, если же прореагируют 1,5 моль водорода и 0,5 моль азота, то Dl =0,5.
к моменту установления равновесия прореагируют 3 моль водорода и 1 моль азота, то Dl =1, если же прореагируют 1,5 моль водорода и 0,5 моль азота, то Dl =0,5.
Из соотношений (I,55) следует: 
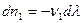
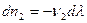 ...
...
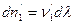
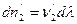 ... или в общем виде
... или в общем виде 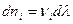
Итак, принимая во внимание, что при химических превращениях происходит изменение внутренней энергии системы, связанное с тем, что внутренняя энергия продуктов реакции отличается от внутренней энергии исходных веществ, представляется удобным и оправданным выделить ту составляющую внутренней энергии, которая обусловлена этими превращениями. Тот факт, что изменение химической переменной Dl оказывается одинаковым для всех участников реакции, позволяет нам при протекании химической реакции рассматривать внутреннюю энергию как функцию лишь одной новой дополнительной переменной – степени превращения l: 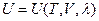 , а не функцию числа молей всех участников реакции
, а не функцию числа молей всех участников реакции 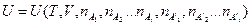 . Такой подход представляется наиболее удобным, т.к. позволяет минимизировать число используемых переменных.
. Такой подход представляется наиболее удобным, т.к. позволяет минимизировать число используемых переменных.
Тогда:
dU = 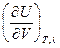 dV +
dV + 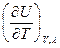 dT +
dT + 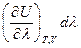 (I, 56)
(I, 56)
δQ = 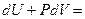
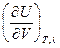 dV +
dV + 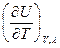 dT +
dT + 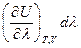 +
+ 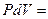
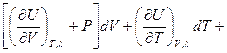
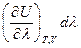 =
= 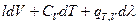 (I,57),
(I,57),
где 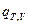 =
= 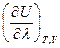 - это тепловой эффект химической реакции, протекающей до конца (D
- это тепловой эффект химической реакции, протекающей до конца (D 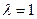 ), при
), при 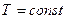 и
и 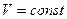 . Он равен изменению внутренней энергии системы.
. Он равен изменению внутренней энергии системы.
При условии протекания в системе химических или фазовых превращений энтальпию также следует рассматривать как функцию 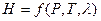 . Тогда:
. Тогда:
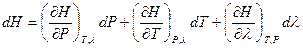 (I,58)
(I,58)
Принимая во внимание определение энтальпии (I, 51) и (I, 31), после дифференцирования можем записать:
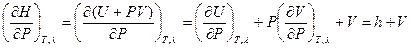 (I, 58а)
(I, 58а)
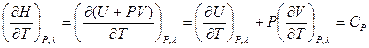 (I, 58б)
(I, 58б)
Если Р = const и l = const, то 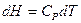
Итак, окончательно получим:
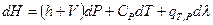 (I,59)
(I,59)
где 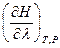 =
= 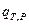 - это тепловой эффект химической реакции, протекающей до конца (D
- это тепловой эффект химической реакции, протекающей до конца (D 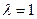 ), при
), при 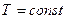 и
и  . Он равен изменению энтальпии системы.
. Он равен изменению энтальпии системы.
Принимая во внимание определение энтальпии (I, 51), также можно записать:
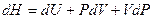
Первые два слагаемых в правой части уравнения по первому закону термодинамики (смотри (I, 7а)) равны 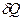 , тогда:
, тогда:
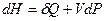 (I, 59а)
(I, 59а)
Следовательно, 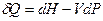 и с учётом (I,59) для элементарной теплоты получаем:
и с учётом (I,59) для элементарной теплоты получаем:
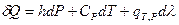
В заключении этого параграфа мы ещё раз вернемся к понятию теплового эффекта химической реакции, которое является одним из важнейших в химической термодинамике.
Дата добавления: 2015-05-21; просмотров: 1257;
