Применение первого закона термодинамики к идеальному газу.
Рассмотрим идеальный газ, т.е. газ, состояние одного моля которого описывается уравнением Менделеева – Клапейрона:
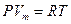 (I, 36)
(I, 36)
где 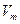 - мольный объём газа, Р и Т – давление и температура соответственно.
- мольный объём газа, Р и Т – давление и температура соответственно.
Состояние идеального газа – это предельное состояние реальных газов при бесконечно малом давлении. Чем выше температура, тем ближе состояние реального газа к идеальному при данном давлении. Однако, свойства реального газа всегда отклоняются от свойств идеального газа, так как уравнение (I, 36) является предельным законом для неосуществимого состояния, при котором давление равно нулю. В применении к реальным газам уравнение (I, 36) является приближенным, согласующимся с действительными свойствами газа тем лучше, чем меньше давление и выше температура.
Другим признаком идеального газа является его подчинение установленному опытным путем закону Гей-Люссака – Джоуля, согласно которому внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма и давления.
Экспериментальное доказательство этого закона было выполнено Джоулем. В калориметр он помещал сосуд, имеющий две камеры А и В, соединенные перекрытой краном трубкой. Он наполнил камеру А газом, а в камере В был создан вакуум. После выравнивания температуры всех частей системы кран открыли. Вследствие этого газ поступал из А в В до тех пор, пока давление в камерах не выравнялось. При этом Джоуль обнаружил лишь очень незначительное изменение температуры. Это означало, что практически не происходил переход тепла от калориметра к камере и наоборот. Предполагается, что если бы этот опыт был выполнен с идеальным газом, то изменения температуры не было бы вовсе.
Применим теперь первый закон термодинамики к описанному выше процессу.
Т.к. Q = 0, то для системы из двух камер и заключенного в них газа имеем:
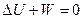 , где
, где 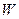 – работа, совершаемая системой и
– работа, совершаемая системой и 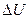 – изменение внутренней энергии системы. Т.к. суммарный объём камер А и В, составляющих систему, не изменился,
– изменение внутренней энергии системы. Т.к. суммарный объём камер А и В, составляющих систему, не изменился, 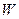 = 0. Поэтому и
= 0. Поэтому и 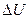 = 0, т.е. энергия системы и, следовательно, газа не изменяется, хотя внутри системы газ сначала занимал только объём А, а в конце процесса заполнял обе камеры А и В. Другими словами, внутренняя энергия идеального газа является функцией только температуры и не зависит от объема и давления.
= 0, т.е. энергия системы и, следовательно, газа не изменяется, хотя внутри системы газ сначала занимал только объём А, а в конце процесса заполнял обе камеры А и В. Другими словами, внутренняя энергия идеального газа является функцией только температуры и не зависит от объема и давления.
Из закона Гей-Люссака – Джоуля следует, что для идеальных газов:
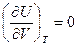 и
и 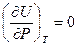
Следовательно, калорический коэффициент l = 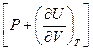 (смотри уравнение (I,25)) в этом случае численно равен внешнему давлению:
(смотри уравнение (I,25)) в этом случае численно равен внешнему давлению:
l = P (I, 37)
Подставив это значение l в уравнение (I, 10) и принимая во внимание, что из уравнения Менделеева-Клапейрона для одного моля идеального газа 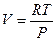 , окончательно получим:
, окончательно получим:
CP – CV = 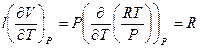 , если принять во внимание постоянство R и P. Таким образом, мы получили известное уравнение Майера, устанавливающего соотношение между мольной теплоёмкостью идеального газа при постоянном давлении и мольной теплоёмкостью газа при постоянном объёме:
, если принять во внимание постоянство R и P. Таким образом, мы получили известное уравнение Майера, устанавливающего соотношение между мольной теплоёмкостью идеального газа при постоянном давлении и мольной теплоёмкостью газа при постоянном объёме:
CP – CV =R (I, 38)
Аналогичным образом найдем значение калорического коэффициента h для идеального газа:
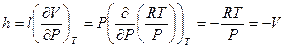 , (I,39)
, (I,39)
если принять во внимание постоянство R и Т.
С учётом полученных результатов выражение первого закона термодинамики через калорические коэффициенты для идеального газа будет иметь следующий вид:
δQ = PdV + CVdT и (I, 40)
dQ = -VdP + CPdT (I,41)
Из кинетической теории газов следует, что:
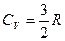 для одноатомных газов (He, Ar, Ne и т.д.)
для одноатомных газов (He, Ar, Ne и т.д.)
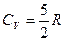 для двухатомных газов (H2, N2, O2, CO и т.д.) и многоатомных газов, имеющих линейное строение (например, СО2, С2Н2 и т.д.)
для двухатомных газов (H2, N2, O2, CO и т.д.) и многоатомных газов, имеющих линейное строение (например, СО2, С2Н2 и т.д.)
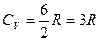 для многоатомных газов нелинейного строения (NH3, CH4, H2S и т.д.)
для многоатомных газов нелинейного строения (NH3, CH4, H2S и т.д.)
Дата добавления: 2015-05-21; просмотров: 1402;
