Диффузия в растворах

Как известно, в смесях газов и в растворах частницы равномерно распределяются по всему объему. Например, если на концентрированный раствор сахара осторожно налить слой чистой воды, то молекулы сахара, совершая хаотическое тепловое движение, постепенно равномерно распределяются по всему объему жидкости. Одновременно и молекулы воды проникают в раствор сахара, разбавляя его. Оба эти процесса идут самопроизвольно и до тех пор, пока не произойдет полного выравнивания концентрации сахара во всем объеме раствора. Самопроизвольный процесс переноса вещества, в результате которого устанавливается равновесное распределение концентраций вследствие беспорядочного теплового движения молекул, атомов и ионов в газах, жидкостях или твердых телах, называется диффузией.Диффузия имеет место и при смешивании растворов различных концентраций, а также в твердых телах и газах. Причем, скорость ее в газах наибольшая, а в твердых телах наименьшая.

Как правило, диффузия частиц совершается из области большей их концентрации в область меньшей концентрации, т, е. количество частиц растворенного вещества, проходящих в единицу времени в сторону меньшей концентрации, Больше, чем в обратном направлении.

Диффузия может быть выражена количественно. Представим себе, что на некотором расстоянии х₁от дна сосуда концентрация растворенного вещества (например, сахара) равна С₁, а на расстоянии х₂. эта концентрация равна С₂. По условию С₁ больше С₂, а х₂ больше х_1, т.е. раствор является более концентрированным у дна сосуда. В на­шем случае градиент концентрации, т. е. изменение концентрации, приходящееся на единицу расстояния, будет равно:

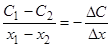
Знак минус в этом уравнении вызван тем, что С₁> С₂.

На основании закона Фика количество растворенного вещества т, которое проходит за время t через воображаемую площадь поперечного сечения сосуда S, находящуюся посередине между концентрациями С₁и С₂, будет равно:

*

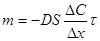где D — коэффициент диффузии, численно равный количеству вещест­ва, диффундирующего за единицу времени через 1 см² поверхности раз­дела при градиенте концентрации, равном 1. Для коэффициента диффу­зии Эйнштейн вывел следующее уравнение:

**

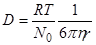где R — универсальная газовая постоянная, Т — абсолютная тем­пература, N₀ — число Авогадро, h — вязкость растворителя, r — радиус диффундирующих частиц.

Объединяя уравнения (*) и (**), получим:

***

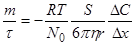где выражение m/t — скорость диффузии, т. е. количество растворен­ного вещества т, проходящего в единицу времени t через площадь се­чения S.

Из уравнения (***) видно, что скорость диффузии возрастает при повышении температуры и градиента концентрации и уменьшается при увеличении вязкости среды и радиуса диффундирующих частиц. Отсюда следует, что вещества с большим молекулярным весом будут иметь сравнительно малые коэффициенты диффузии.