Кинетика ферментативных процессов
Реакция первого порядка
Рассмотрим реакцию первого порядка 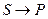 (концентрации равны:
(концентрации равны:  ).
).
Скорость реакции равна 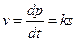 , где k — константа скорости реакции первого порядка. По закону сохранения вещества, суммарная концентрация продукта и субстрата в каждый момент времени равна начальной концентрации субстрата
, где k — константа скорости реакции первого порядка. По закону сохранения вещества, суммарная концентрация продукта и субстрата в каждый момент времени равна начальной концентрации субстрата 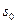 :
: 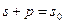 , где
, где 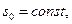 t — время.
t — время.
Итак, имеем уравнение:
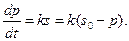 (1.5)
(1.5)
Решая дифференциальное уравнение (1.5) методом разделения переменных, получаем:
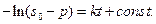 (1.6)
(1.6)
Значение константы const определяется, исходя из начальных условий: при t = 0 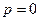 и
и 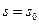 . Таким образом,
. Таким образом, 
Подставляя найденное значение константы в формулу (1.6) и выражая искомое 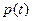 , получаем решение:
, получаем решение:
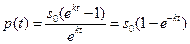 . (1.7)
. (1.7)
Пример1.7. Определите константу скорости реакции, если 99% субстрата перешло в продукт через 5 секунд после начала реакции.
Решение: Переход 99-ти процентов субстрата в продукт означает, что 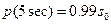 . Подставляем в формулу (1.7):
. Подставляем в формулу (1.7):
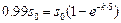 ,
,
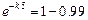 ,
,
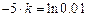 ,
,
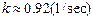 .
.
РеакцияМихаэлиса-Ментен
Рассмотрим базовую модель ферментативной реакции, предложенной Михаэлисом и Ментен. Цель исследования – определить скорость реакции, катализируемой ферментом. Схема реакции:  .
.
Субстрат S образует с ферментом E фермент-субстратный комплекс ES (реакция обратимая); затем этот комплекс распадается на фермент и продукт P (реакция необратимая); 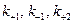 – константы скоростей реакций.
– константы скоростей реакций.
Искомая скорость – скорость реакции  :
:  .
.
Итак, пусть x – концентрация комплекса ES; e0 – суммарное количество фермента, участвующего в реакции; s концентрация субстрата. Тогда
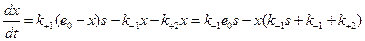 . (1.8)
. (1.8)
Пусть концентрация субстрата значительно превышает концентрацию фермента. Это значит, что в системе будет достигаться квазистационарное состояние, в котором концентрация фермент-субстратного комплекса постоянна, или 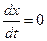 . Тогда из уравнения (1.8) получаем:
. Тогда из уравнения (1.8) получаем:
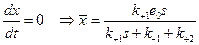 .
.
Скорость образования продукта в условиях постоянной концентрации фермент-субстратного комплекса равна: 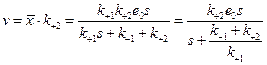 . Введем обозначения:
. Введем обозначения: 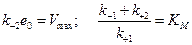 . Тогда выражение для скорости протекания реакции по механизму Михаэлиса-Ментен принимает вид:
. Тогда выражение для скорости протекания реакции по механизму Михаэлиса-Ментен принимает вид:
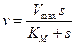 — уравнение Михаэлиса-Ментен.
— уравнение Михаэлиса-Ментен.
Величина 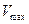 — максимальная скорость протекания реакции (весь фермент связан в комплекс). Величина
— максимальная скорость протекания реакции (весь фермент связан в комплекс). Величина 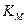 называется константой Михаэлиса. При
называется константой Михаэлиса. При 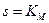 скорость реакции равна половине максимальной.
скорость реакции равна половине максимальной.
Пример1.8. Постройте график зависимости скорости протекания ферментативной реакции по механизму Михаэлиса-Ментен v в зависимости от величины v/s. Как определить по графику  и
и 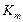 ? Чему соответствуют точки пересечения с осями?
? Чему соответствуют точки пересечения с осями?
Решение: Запишем уравнение Михаэлиса-Ментен: 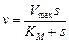 . Умножим обе части уравнения на выражение
. Умножим обе части уравнения на выражение 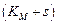 и раскроем скобки:
и раскроем скобки:  . Делим обе части на
. Делим обе части на 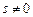 :
:
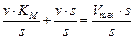 ,
, 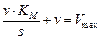 ,
, 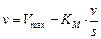 . Получили зависимость
. Получили зависимость 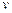 от аргумента
от аргумента 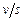 . Эта зависимость является линейной функцией, на графике изображается прямой (рис.1.6) с отрицательным углом наклона, тангенс которого равен
. Эта зависимость является линейной функцией, на графике изображается прямой (рис.1.6) с отрицательным углом наклона, тангенс которого равен 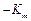 . При
. При 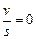
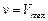 . Скорость
. Скорость 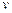 будет равняться нулю при
будет равняться нулю при 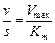 .
.
Рис. 1.6. График зависимости скорости v протекания реакции по механизму Михаэлис-Ментен от отношения v/s (пример 3.2.)
Задачи
1.1. Найдите стационарные состояния уравнений:
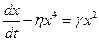 ;
; 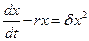 ;
;
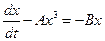 ;
; 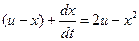 ;
;
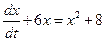 ;
;  .
.
1.2. Разложите функцию 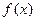 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 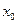 до 4 порядка:
до 4 порядка:
 ,
, 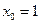 ;
;  ,
, 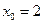 ;
;
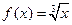 ,
, 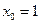 ;
; 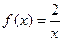 ,
, 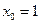 ;
;
 ,
, 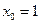 ;
; 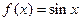 ,
, 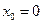 .
.
1.3. Пусть  . Определите по графику функции
. Определите по графику функции 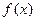 устойчивость всех стационарных состояний системы.
устойчивость всех стационарных состояний системы.
| а) File: task1_3_a_a | б) File: task1_3_b_б |
| в) File: task1_3_с_в | г) File: task1_3_d_г |
1.4. Пусть  . Найти стационарные состояния уравнения и определить их тип устойчивости с помощью графика функции
. Найти стационарные состояния уравнения и определить их тип устойчивости с помощью графика функции 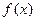 :
:
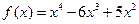 ;
; 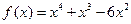 .
.
1.5. Пусть 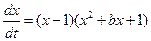 . Постройте график зависимости величины стационарного значения переменной x от значений параметра b. Сколько стационарных состояний имеет уравнение при
. Постройте график зависимости величины стационарного значения переменной x от значений параметра b. Сколько стационарных состояний имеет уравнение при 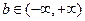 ?
?
1.6. Определите тип особой точки системы линейных уравнений:
а) 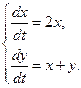 ; б)
; б)  ; в)
; в) 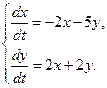 ; г)
; г) 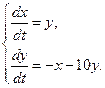 ; д)
; д) 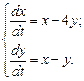
1.7. Постройте фазовый портрет для каждой из систем задачи 1.6 в окрестности стационарного состояния: а) отметьте стационарные точки на фазовой плоскости; б) постройте главные изоклины; в) по главным изоклинам постройте несколько интегральных кривых с различными начальными условиями; г) стрелкой укажите направление движения изображающей точки вдоль интегральных кривых при 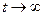 .
.
1.8. Постройте фазовую траекторию в окрестности стационарной точки, соответствующую кинетическим кривым, изображенным на рисунке. Определите тип стационарного состояния. 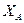 ,
, 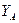 – начальные условия
– начальные условия
а)
File: task1_8_a_a
б)
File: task1_8_b_б
в)
File: task1_8_c_в
г)
File: task1_8_d_г
1.9. Постройте в едином масштабе времени кинетические кривые, соответствующие фазовой траектории с начальными условиями в т. А. Укажите тип особой точки:
a)
File: task1_9_a_a
б)
File: task1_9_b_б
в)
File: task1_9_c_в
г)
File: task1_9_d_г
1.10. Проведите линеаризацию системы дифференциальных уравнений в окрестности нулевого стационарного состояния и определите его тип устойчивости:
а) 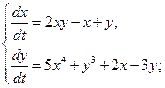 б)
б) 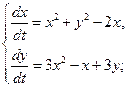
в) 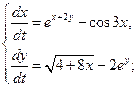 г)
г) 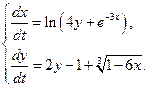
1.11. Проведите полный анализ систем уравнений: 1) найдите стационарные состояния; 2) линеаризуйте системы в окрестностях стационарных состояний; 3) определите тип устойчивости стационарных состояний; 4) постройте фазовые портреты.
модель взаимоотношений типа хищник-жертва
а) 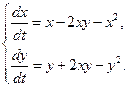 б)
б) 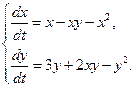
модель конкуренции одинаковых видов с учетом внутривидовой конкуренции
в) 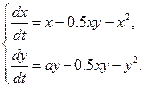 г)
г) 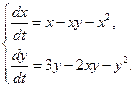
1.12.Определите тип стационарных состояний на всей плоскости допустимых значений параметров. Укажите область значений параметров, в которой возможно существование предельного цикла.
модель брюсселятора (биохимический осциллятор)
а) 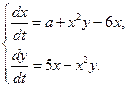
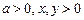 ; б)
; б) 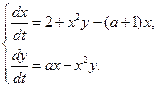
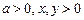 ;
;
модель гликолиза
в) 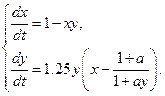
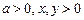 ; г)
; г) 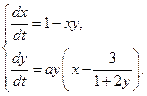
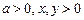 ;
;
модель генератора Ван дер Поля
д) 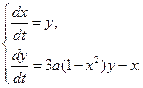
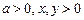 .
.
1.13. Определите константу скорости реакции первого порядка, если 99% субстрата перешло в продукт через 5 секунд после начала реакции?
1.14. В реакции первого порядка начальная концентрация субстрата равна 1мМ. Какое количество субстрата прореагировало за первую секунду, если константа скорости реакции равна 1с-1?
1.15. Концентрация субстрата в начале реакции равна 5 мМ, константа скорости реакции первого порядка равна 0,5с-1. Постройте график зависимости логарифма концентрации субстрата от времени. Укажите координаты точек пересечения графика с осями.
1.16. В ходе реакции первого порядка за первые 3с образовалось 3мМ продукта. Определите начальную концентрацию субстрата, если известно, что константа скорости реакции равна 0,01с-1.
1.17. Максимальная скорость реакции по Михаэлису – Ментен равна 10единицам. Константа Михаэлиса равна 0,5единиц. Постройте график зависимости скорости протекания реакцииот начальной концентрации субстрата в координатах:
а) 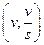 ;
;
б) 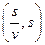 ;
;
в) 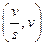 ;
;
г) 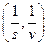 .
.
Как определить по графику 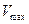 и
и 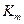 ? Чему соответствуют точки пересечения графика с осями координат (в общем виде и численно)?
? Чему соответствуют точки пересечения графика с осями координат (в общем виде и численно)?
1.18. Определите с помощью графика параметры уравнения Михаэлиса – Ментен. Укажите размерности переменных и параметров, входящих в уравнение Михаэлиса – Ментен.
| а) File: task1_18_a_a | б) File: task1_18_b_б |
| в) File: task1_18_c_в | г) File: task1_18_d_г |
Дата добавления: 2015-06-22; просмотров: 2202;
