Качественные методы исследования динамических моделей
КИНЕТИКА БИОЛОГИЧЕСКИХ ПРОЦЕССОВ
Как можно описать динамику биологических систем? В каждый момент времени биологическая система обладает набором некоторых характеристик. Например, наблюдая за популяцией какого-то вида, можно регистрировать ее численность, площадь занимаемой территории, количество доступного питания, температуру окружающей среды и т. д. Протекание химической реакции можно характеризовать концентрациями участвующих веществ, давлением, температурой, уровнем кислотности среды. Совокупность значений всех характеристик, которые исследователь выбрал для описания системы, является состоянием системы в каждый момент времени. При создании модели в указанной совокупности выделяют переменные и параметры. Переменные – это те величины, изменения которых в первую очередь интересует исследователя, параметры – условия «внешней среды». Именно для выбранных переменных составляют уравнения, отражающие закономерности изменения системы во времени. Например, при создании модели роста культуры микроорганизмов, в качестве переменной обычно выступает ее численность, а в качестве параметра – скорость размножения. Возможно, существенной окажется температура, при которой происходит рост, тогда этот показатель также включается в модель в качестве параметра. А если, например, уровень аэрации всегда является достаточным и не оказывает никакого влияния на ростовые процессы, тогда его вообще не включают в модель. Как правило, параметры остаются неизменными во время эксперимента, однако стоит отметить, что это не всегда так.
Описывать динамику биологической системы (то есть изменение ее состояния во времени) можно как дискретными, так и непрерывными моделями. В дискретных моделях предполагается, что время представляет собой дискретную величину. Это соответствует регистрации значений переменных через определенные фиксированные интервалы времени (например, раз в час или раз в год). В непрерывных моделях биологическая переменная является непрерывной функцией времени, обозначаемой, например, x(t).
Часто большое значение имеют начальные условия модели – состояние исследуемой характеристики в начальный момент времени, т.е. при t = 0.
При изучении непрерывного изменения некоторой характеристики x(t) нам может быть известна информация о скорости ее изменения  . Эта информация в общем случае может быть записана в виде дифференциального уравнения:
. Эта информация в общем случае может быть записана в виде дифференциального уравнения:
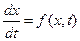 . (1.1)
. (1.1)
Такая формальная запись означает, что скорость изменения некоторой исследуемой характеристики  является функцией времени и величины этой характеристики
является функцией времени и величины этой характеристики  .
.
Если правая часть дифференциального уравнения вида 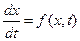 явно не зависит от времени, т.е. справедливо:
явно не зависит от времени, т.е. справедливо:
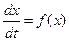 ,
,
то такое уравнение называется автономным (система, описываемая таким уравнением, называется автономной). Состояние автономных систем в каждый момент времени характеризуется одной единственной величиной — значением переменной x в данный момент времени t.
Зададимся вопросом: пусть дано дифференциальное уравнение для x(t), можно ли найти все функции x(t), удовлетворяющие этому уравнению? Или: если известно начальное значение некоторой переменной (например, начальный размер популяции, концентрация вещества, электропроводность среды и т.п.) и имеется информация о характере изменения этой переменной, то можно ли предсказать, каким будет ее значение во все последующие моменты времени? Ответ на поставленный вопрос звучит следующим образом: если заданы начальные условия 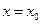 при
при 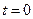 и для уравнения выполнены условия теоремы Коши (функция
и для уравнения выполнены условия теоремы Коши (функция  , заданная в некоторой области, и ее частная производная
, заданная в некоторой области, и ее частная производная  непрерывны в этой области), то имеется единственное решение уравнения, удовлетворяющее заданным начальным условиям. (Напомним, что любая непрерывная функция, которая удовлетворяет дифференциальному уравнению, называется решением этого уравнения.) Это означает, что мы можем однозначно предсказывать поведение биологической системы, если известны характеристики ее начального состояния, и уравнение модели удовлетворяет условиям теоремы Коши.
непрерывны в этой области), то имеется единственное решение уравнения, удовлетворяющее заданным начальным условиям. (Напомним, что любая непрерывная функция, которая удовлетворяет дифференциальному уравнению, называется решением этого уравнения.) Это означает, что мы можем однозначно предсказывать поведение биологической системы, если известны характеристики ее начального состояния, и уравнение модели удовлетворяет условиям теоремы Коши.
Стационарное состояние. Устойчивость
Будем рассматривать автономное дифференциальное уравнение
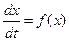 . (1.2)
. (1.2)
В стационарном состоянии значения переменных в системе не меняются со временем, то есть скорость изменения значений переменных  равна 0:
равна 0: 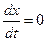 . Если левая часть уравнения (1.2) равна нулю, то и правая тоже равна нулю:
. Если левая часть уравнения (1.2) равна нулю, то и правая тоже равна нулю: 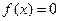 . Корни этого алгебраического уравнения
. Корни этого алгебраического уравнения 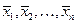 являются стационарными состояниями дифференциального уравнения (1.2).
являются стационарными состояниями дифференциального уравнения (1.2).
Пример1.1: Найдите стационарные состояния уравнения  .
.
Решение: Перенесем слагаемое, не содержащее производную, в правую часть равенства: 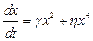 . По определению в стационарном состоянии
. По определению в стационарном состоянии 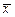 выполняется равенство:
выполняется равенство:  . Значит, должно выполняться равенство
. Значит, должно выполняться равенство  . Решаем уравнение:
. Решаем уравнение:
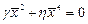 ,
,
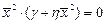 ,
,
 или
или 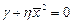 ,
,
 или
или  ,
,
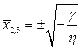 .
.
Итак, уравнение имеет 3 стационарных состояния:  ,
, 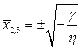 .
.
Биологические системы постоянно испытывают различные внешние воздействия и многочисленные флуктуации. При этом они (биологические системы) обладают гомеостазом, т.е. устойчивы. На математическом языке это означает, что переменные при малых отклонениях возвращаются к своим стационарным значениям. Будет ли отражать такой характер поведения биологической системы ее математическая модель? Устойчивы ли стационарные состояния модели?
Стационарное состояние является устойчивым, если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки. Устойчивое состояние соответствует устойчивому режиму функционирования системы.
Состояние равновесия 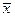 уравнения
уравнения 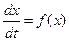 устойчиво по Ляпунову, если для любого
устойчиво по Ляпунову, если для любого  всегда можно найти такое
всегда можно найти такое 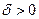 , что если
, что если 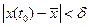 , то
, то 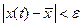 для всех
для всех  .
.
Существует аналитический метод исследования устойчивости стационарного состояния – метод Ляпунова. Для его обоснования напомним формулу Тейлора.
Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Пусть функция 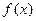 имеет в точке
имеет в точке 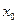 производные всех порядков до n-го включительно. Тогда для
производные всех порядков до n-го включительно. Тогда для 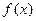 справедлива формула Тейлора:
справедлива формула Тейлора:
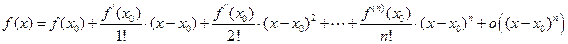 .
.
Отбросив остаточный член  , который представляет себя бесконечно малую более высокого порядка, чем
, который представляет себя бесконечно малую более высокого порядка, чем  , получим приближенную формулу Тейлора:
, получим приближенную формулу Тейлора:
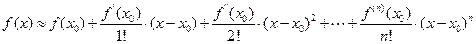 .
.
Правая часть приближенной формулы называется многочленом Тейлора функции 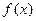 , его обозначают как
, его обозначают как 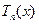 .
.
Пример1.2: Разложите функцию 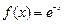 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 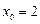 до 4 порядка.
до 4 порядка.
Решение: Запишем ряд Тейлора до 4-го порядка в общем виде:
 .
.
Найдем производные заданной функции в точке 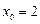 :
:
 ,
,
 ,
,
 ,
,
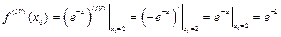 .
.
Подставим полученные значения в исходную формулу:
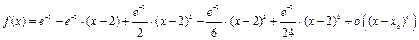 .
.
Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова) состоит в следующем. Пусть 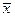 – стационарное состояние уравнения
– стационарное состояние уравнения 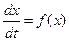 . Зададим небольшое отклонение переменной x от ее стационарного значения:
. Зададим небольшое отклонение переменной x от ее стационарного значения:  , где
, где 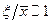 . Подставим выражение для точки x в исходное уравнение:
. Подставим выражение для точки x в исходное уравнение: 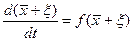 . Левая часть уравнения примет вид:
. Левая часть уравнения примет вид:  , поскольку в стационарном состоянии скорость изменения значения переменой равна нулю:
, поскольку в стационарном состоянии скорость изменения значения переменой равна нулю: 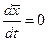 . Правую часть разложим в ряд Тейлора в окрестности стационарного состояния, учитывая, что
. Правую часть разложим в ряд Тейлора в окрестности стационарного состояния, учитывая, что 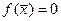 , оставим только линейный член в правой части уравнения:
, оставим только линейный член в правой части уравнения:
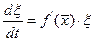 .
.
Получили линеаризованное уравнение или уравнение первого приближения. Величина 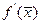 есть некоторая постоянная величина, обозначим ее a:
есть некоторая постоянная величина, обозначим ее a: 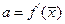 . Общее решение линеаризованного уравнения имеет вид:
. Общее решение линеаризованного уравнения имеет вид: 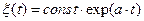 . Это выражение описывает закон, по которому будет изменяться во времени заданное нами отклонение от стационарного состояния
. Это выражение описывает закон, по которому будет изменяться во времени заданное нами отклонение от стационарного состояния 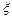 . Отклонение будет со временем затухать, т.е.
. Отклонение будет со временем затухать, т.е.  при
при 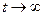 , если показатель степени в экспоненте будет отрицательным, т.е.
, если показатель степени в экспоненте будет отрицательным, т.е. 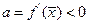 . По определению стационарное состояние
. По определению стационарное состояние 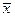 будет устойчивым. Если же
будет устойчивым. Если же 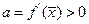 , то с увеличением времени отклонение будет только увеличиваться, стационарное состояние – неустойчивое. В случае, когда
, то с увеличением времени отклонение будет только увеличиваться, стационарное состояние – неустойчивое. В случае, когда 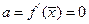 уравнение первого приближения ответа на вопрос об устойчивости стационарного состояния дать не может. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора.
уравнение первого приближения ответа на вопрос об устойчивости стационарного состояния дать не может. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора.
Кроме аналитического метода исследования устойчивости стационарного состояния существует и графический.
Пример1.3. Пусть  . Найти стационарные состояния уравнения и определить их тип устойчивости с помощью графика функции
. Найти стационарные состояния уравнения и определить их тип устойчивости с помощью графика функции 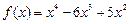 .
.
Решение: Найдем особые точки:
 ,
,
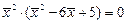 ,
,
 или
или 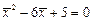 ,
,
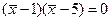 ,
,
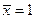 или
или 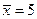 .
.
Строим график функции 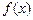 (рис.1.1).
(рис.1.1).
Рис. 1.1. График функции 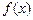 (пример 1.3).
(пример 1.3).
Определим по графику устойчиво ли каждое из найденных стационарных состояний. Зададим небольшое отклонение изображающей точки от особой точки  влево:
влево:  . В точке с координатой
. В точке с координатой  функция
функция 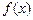 принимает положительное значение:
принимает положительное значение: 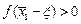 или
или 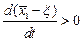 . Последнее неравенство означает, что со временем координата
. Последнее неравенство означает, что со временем координата  должна увеличиваться, то есть изображающая точка должна возвратиться к точке
должна увеличиваться, то есть изображающая точка должна возвратиться к точке  . Теперь зададим небольшое отклонение изображающей точки от особой точки
. Теперь зададим небольшое отклонение изображающей точки от особой точки  вправо:
вправо: 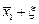 . В этой области функция
. В этой области функция 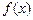 сохраняет положительное значение, следовательно, со временем координата x также увеличивается, то есть изображающая точка будет отдаляться от точки
сохраняет положительное значение, следовательно, со временем координата x также увеличивается, то есть изображающая точка будет отдаляться от точки  . Таким образом, малое отклонение
. Таким образом, малое отклонение 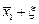 выводят систему из стационарного состояния, следовательно, по определению особая точка
выводят систему из стационарного состояния, следовательно, по определению особая точка  неустойчива. Аналогичные рассуждения приводят к тому, что любое отклонение от особой точки
неустойчива. Аналогичные рассуждения приводят к тому, что любое отклонение от особой точки 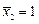 со временем затухает, стационарное состояние
со временем затухает, стационарное состояние 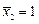 устойчиво. Отклонение изображающей точки в любом направлении от стационарного состояния
устойчиво. Отклонение изображающей точки в любом направлении от стационарного состояния 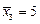 приводит к ее удалению от точки
приводит к ее удалению от точки 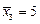 , это неустойчивое стационарное состояние.
, это неустойчивое стационарное состояние.
Решение системы линейных дифференциальных уравнений
Перейдем к изучению систем уравнений, сначала линейных. В общем виде систему линейных дифференциальных уравнений можно представить в виде:
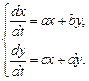 (1.3)
(1.3)
Анализ системы уравнений начинается с нахождения стационарных состояний. У систем вида (1.3) особая точка единственна, ее координаты – (0,0). Исключение составляет вырожденный случай, когда уравнения можно представить в виде:
 (1.3*)
(1.3*)
В этом случае все пары  , удовлетворяющие соотношению
, удовлетворяющие соотношению 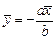 , являются стационарными точками системы (1.3*). В частности, точка (0,0) также является стационарной для системы (1.3*). На фазовой плоскости в данном случае имеем прямую с коэффициентом наклона
, являются стационарными точками системы (1.3*). В частности, точка (0,0) также является стационарной для системы (1.3*). На фазовой плоскости в данном случае имеем прямую с коэффициентом наклона  , проходящую через начало координат, каждая точка которой является особой точкой системы (1.3*) (см. таблицу1.1, пункт 6).
, проходящую через начало координат, каждая точка которой является особой точкой системы (1.3*) (см. таблицу1.1, пункт 6).
Основной вопрос, на который должен отвечать результат исследования системы уравнений: устойчиво ли стационарное состояние системы, и какой характер имеет это решение (монотонный или немонотонный).
Общее решение системы двух линейных уравнений имеет вид:
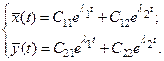
Характеристические числа 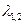 могут быть выражены через коэффициенты линейных уравнений следующим образом:
могут быть выражены через коэффициенты линейных уравнений следующим образом:

Характеристические числа могут быть 1) действительными разных знаков, 2) действительными одного знака, 3) комплексно сопряженными, а также, в вырожденных случаях, 4) чисто мнимыми, 5) действительными совпадающими, 6) действительными, один из которых (или оба) равен нулю. Эти случаи определяют тип поведения решения системы обыкновенных дифференциальных уравнений. Соответствующие фазовые портреты представлены в таблице1.1.
Таблица 1.1. Типы стационарных состояний системы двух линейных дифференциальных уравнений и соответствующие фазовые портреты. Стрелками показано направление движения изображающей точки
1. 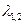 – действительные, разных знаков – действительные, разных знаков
|
| File: table1_1r1c1 седло |
2. 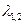 – действительные, одного знака – действительные, одного знака
| |
File: table1_1r2c1
неустойчивый узел
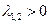
| File: table1_1r2c2
устойчивый узел
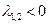
|
3. 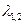 – комплексные, вещественная часть отлична от нуля – комплексные, вещественная часть отлична от нуля
| |
File: table1_1r3c1
неустойчивый фокус 
| File: table1_1r3c2
устойчивый фокус 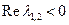
|
4. 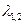 – чисто мнимые – чисто мнимые
|
| File: table1_1r4c1 центр |
5. 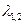 – действительные, совпадающие – действительные, совпадающие
| |
File: table1_1r5c1
дикритический узел
устойчивый или неустойчивый, система имеет вид 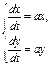
| File: table1_1r5c2 вырожденный узел устойчивый или неустойчивый |
6.  – действительный, – действительный,  или или 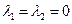
| |
File: table1_1r6c1
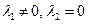 особыми точками являются все точки прямой
особыми точками являются все точки прямой 
| File: table1_1r6c2
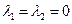 каждая точка фазовой плоскости является особой
каждая точка фазовой плоскости является особой
|
Построение фазовых и кинетических портретов системы двух линейных дифференциальных уравнений
Фазовой плоскостью называется плоскость с осями координат, на которых отложены значения переменных x и y, каждая точка плоскости соответствует определенному состоянию системы. Совокупность точек на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных 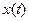 ,
, 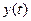 согласно заданным уравнениям исследуемой системы, называется фазовой траекторией. Совокупность фазовых траекторий при различных начальных значениях переменных дает портрет системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x и y без знания аналитических решений исходной системы уравнений.
согласно заданным уравнениям исследуемой системы, называется фазовой траекторией. Совокупность фазовых траекторий при различных начальных значениях переменных дает портрет системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x и y без знания аналитических решений исходной системы уравнений.
Рассмотрим систему линейных дифференциальных уравнений:
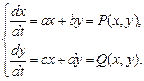
Построение фазового портрета начинаем с построения главных изоклин (изоклина – линия, на всём протяжении которой наклон фазовой кривой (траектории), определяемый уравнением, сохраняет постоянное значение). Для системы двух линейных дифференциальных уравнений – это всегда прямые, проходящие через начало координат. Уравнение изоклины горизонтальных касательных:  . Уравнение изоклины вертикальных касательных:
. Уравнение изоклины вертикальных касательных: 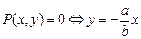 . Для дальнейшего построения фазового портрета полезно построить изоклину касательных, проходящих под углом
. Для дальнейшего построения фазового портрета полезно построить изоклину касательных, проходящих под углом 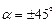 . Для нахождения соответствующего уравнения изоклины необходимо решить уравнение
. Для нахождения соответствующего уравнения изоклины необходимо решить уравнение 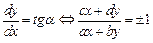 . Можно находить и изоклины касательных других углов, пользуясь приблизительными значениями тангенсов углов. В построении фазового портрета также может помочь ответ на вопрос, под каким углом фазовые траектории должны пересекать координатные оси. Для этого в уравнение изоклины
. Можно находить и изоклины касательных других углов, пользуясь приблизительными значениями тангенсов углов. В построении фазового портрета также может помочь ответ на вопрос, под каким углом фазовые траектории должны пересекать координатные оси. Для этого в уравнение изоклины  подставляем соответствующие равенства
подставляем соответствующие равенства  (для определения угла пересечения с оcью OY) и
(для определения угла пересечения с оcью OY) и  (для определения угла пересечения с оcью OХ).
(для определения угла пересечения с оcью OХ).
Пример1.4. Определите тип особой точки системы линейных уравнений:

Постройте фазовый и кинетический портрет системы.
Решение: Координаты особой точки – (0,0). Коэффициенты линейных уравнений равны:  ,
, 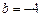 ,
, 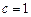 ,
, 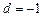 . Определим тип стационарного состояния (см. раздел о характеристических числах):
. Определим тип стационарного состояния (см. раздел о характеристических числах):

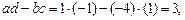
 .
.
Таким образом, характеристические корни являются мнимыми: 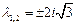 , следовательно, особая точка рассматриваемой линейной системы имеет тип центр (рис. 1.2а).
, следовательно, особая точка рассматриваемой линейной системы имеет тип центр (рис. 1.2а).
Уравнение изоклины горизонтальных касательных: 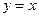 , уравнение изоклины вертикальных касательных:
, уравнение изоклины вертикальных касательных:  . Под углом в 45° траектории системы пересекают прямую
. Под углом в 45° траектории системы пересекают прямую 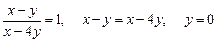 .
.
После построения фазового портрета необходимо определить направление движения по найденным траекториям. Это можно сделать следующим образом. Возьмем произвольную точку на любой траектории. Например, на изоклине горизонтальных касательных (1,1). Подставим координаты этой точки в систему уравнений. Получим выражения для скоростей изменения переменных x, y в этой точке:
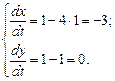
Полученные значения показывают, что скорость изменения переменной x – отрицательная, то есть ее значение должно уменьшаться, а переменная y не изменяется. Отмечаем полученное направление стрелкой. Таким образом, в рассматриваемом примере движение по фазовым траекториям направлено против часовой стрелки. Подставляя в систему координаты разных точек можно получить «карту» направлений скоростей, так называемое векторное поле.
Рис 1.2. Фазовый (а) и кинетический (б) портрет системы, пример 1.4
Отметим, что на изоклине горизонтальных касательных переменная y достигает своего максимального или минимального значения на данной траектории. Наоборот, на изоклине вертикальных касательных, своего максимального по модулю значения для выбранной траектории достигает переменная x.
Построить кинетический портрет системы означает построить графики зависимости величин переменных x, y от времени. По фазовому портрету можно построить кинетический и наоборот. Одной фазовой траектории соответствует одна пара кинетических кривых. Выберем на фазовом портрете произвольную точку на произвольной фазовой траектории. Это начальная точка, соответствующая моменту времени 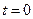 . В зависимости от направления движения в рассматриваемой системе значения переменных x, y либо уменьшаются, либо увеличиваются. Пусть координаты начальной точки – (1,1). Согласно построенному фазовому портрету, стартуя из этой точки, мы должны двигаться против часовой стрелки, координаты x и y при этом будут уменьшаться. С течением времени координата x проходит через 0, значение y при этом остается положительным. Далее координаты x и y продолжают уменьшаться, координата y проходит через 0 (значение x при этом отрицательно). Величина x достигает минимального значения на изоклине вертикальных касательных, затем начинает увеличиваться. Величина y своего минимального значения достигает на изоклине горизонтальных касательных (значение x в этот момент времени отрицательно). Далее и величина x, и величина y увеличиваются, возвращаясь к начальным значениям (рис. 1.2б).
. В зависимости от направления движения в рассматриваемой системе значения переменных x, y либо уменьшаются, либо увеличиваются. Пусть координаты начальной точки – (1,1). Согласно построенному фазовому портрету, стартуя из этой точки, мы должны двигаться против часовой стрелки, координаты x и y при этом будут уменьшаться. С течением времени координата x проходит через 0, значение y при этом остается положительным. Далее координаты x и y продолжают уменьшаться, координата y проходит через 0 (значение x при этом отрицательно). Величина x достигает минимального значения на изоклине вертикальных касательных, затем начинает увеличиваться. Величина y своего минимального значения достигает на изоклине горизонтальных касательных (значение x в этот момент времени отрицательно). Далее и величина x, и величина y увеличиваются, возвращаясь к начальным значениям (рис. 1.2б).
Исследование устойчивости стационарных состояний нелинейных систем второго порядка
Пусть биологическая система описывается системой двух автономных дифференциальных уравнения второго порядка общего вида:
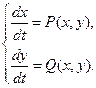
Стационарные значения переменных системы определяются из алгебраических уравнений:
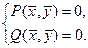
В окрестности каждого стационарного состояния можно рассмотреть систему первого приближения (линеаризованную систему), исследование которой может позволить ответить на вопрос об устойчивости особой точки и о характере фазовых траекторий в ее малой окрестности.
Пусть  и
и 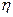 – некоторые смещения от стационарного состояния
– некоторые смещения от стационарного состояния  . Тогда линеаризованная система, описывающая изменение во времени этих смещений, будет иметь вид:
. Тогда линеаризованная система, описывающая изменение во времени этих смещений, будет иметь вид:
 (1.4)
(1.4)
Введем обозначения: 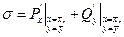 ,
, 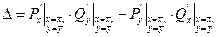 . Особые точки, у которых
. Особые точки, у которых 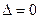 или
или  , называются негрубыми. Характер негрубых состояний равновесия (в частности, устойчивость) не определяется значениями коэффициентов системы первого приближения.
, называются негрубыми. Характер негрубых состояний равновесия (в частности, устойчивость) не определяется значениями коэффициентов системы первого приближения.
Для грубых состояний равновесия (то есть для всех точек плоскости параметров 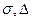 , лежащих вне оси
, лежащих вне оси 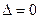 и полуоси
и полуоси  ) тип поведения системы определяется из анализа линейной системы (1.4).
) тип поведения системы определяется из анализа линейной системы (1.4).
Пример1.5. Проведите линеаризацию системы уравнений в окрестности нулевого стационарного состояния и определите его тип устойчивости:
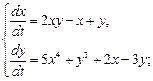
Решение: Для линеаризации системы уравнений в окрестности нулевого стационарного состояния найдем частные производные функций в правых частях уравнений, в качестве координаты стационарного состояния 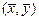 подставим значения
подставим значения 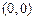 .
.
 ,
, 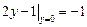 ;
;
 ,
,  ;
;
 ,
,  ;
;
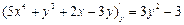 ,
,  .
.
Имеем,  ,
, 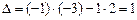 , особая точка грубая. Характеристические корни системы первого приближения равны
, особая точка грубая. Характеристические корни системы первого приближения равны 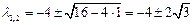 , оба действительны и отрицательны, следовательно, в окрестности нулевой особой точки поведение фазовых траекторий системы будет соответствовать типу устойчивый узел.
, оба действительны и отрицательны, следовательно, в окрестности нулевой особой точки поведение фазовых траекторий системы будет соответствовать типу устойчивый узел.
Дата добавления: 2015-06-22; просмотров: 1835;
