Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания)
Рассмотрим, как влияет на свободные колебания сопротивления среды, считая, что сила сопротивления пропорциональна первой степени скорости: 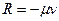 .
.
(«–» указывает, что R против v). Пусть на точку при её движении действует восстанавливающая сила 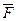 и сила сопротивления
и сила сопротивления 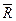 .
.
Тогда 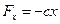
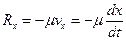 .
.
Дифференциальное уравнение будет 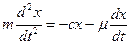
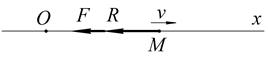
Рис. 3.11
Деля обе части на m, получим:
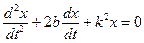 (38)
(38)
где обозначено
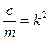 ,
, 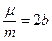 (39)
(39)
Уравнение (38) представляет собой дифференциальное уравнение 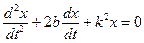 . Общее решение уравнения ( 38) имеет вид
. Общее решение уравнения ( 38) имеет вид
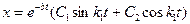 (40)
(40)
или по аналогии с равенством (30)
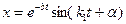 (41)
(41)
Входящая сюда постоянная и являются постоянными интегрирования и определяются по начальным условиям.
Колебания, проходящие по закону (38) называют затухающими, т.к. благодаря множителю 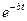 величина
величина 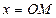 с течением времени убывает, стремясь к нулю.
с течением времени убывает, стремясь к нулю.
Промежуток времени 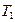 , равный периоду
, равный периоду 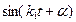 т.е. величину
т.е. величину
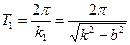 (42)
(42)
принято называть периодом затухающих колебаний.
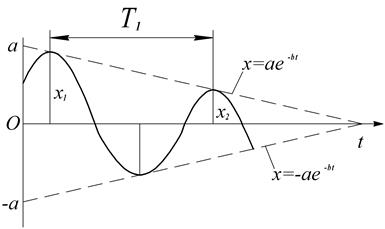
Рис. 3.12
Формулу (42), если учесть равенство (35), можно представить в виде:
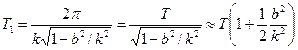 (42/)
(42/)
Из 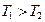 формул видно, что наличие сопротивления увеличивает период колебаний. Однако, когда сопротивление мало
формул видно, что наличие сопротивления увеличивает период колебаний. Однако, когда сопротивление мало 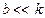 , то величиной
, то величиной 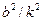 по сравнению с единицей можно пренебречь и считать
по сравнению с единицей можно пренебречь и считать 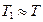 .
.
Дата добавления: 2015-06-17; просмотров: 1016;
