Теорема об изменении момента количества движения

(теорема моментов).

Иногда при изучении движения точки вместо изменения самого вектора (m 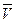) оказывается необходимым рассматривать изменение его момента. Момент вектора m 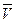относительно данного центра О или оси z обозначается 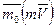и и 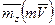называется моментом количества движения или кинетическим моментом точки относительно этого центра (оси). Вычисляется момент вектора m 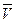так же, как и момент силы. При этом вектор m 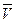считается приложенным к движущей точке. По модулю 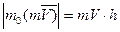, где h – длина перпендикуляра, опущенного из центра О на направление вектора m .

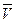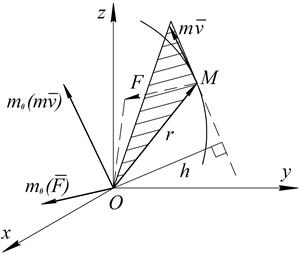
Рис. 3.6

Теорема моментов относительно оси.

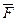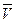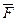Рассмотрим материальную точку массы m, движущуюся под действием силы . Найдем для нее зависимость между моментами векторов m и относительно какой-либо неподвижной оси z. По полученным ранее формулам (статика)

(*)

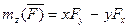Аналогично и для момента 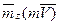, если вынести m за скобку

.

Беря от обеих частей этого равенства производные по времени, находим:

.

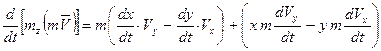В первой части первая скобка равна 0, так как .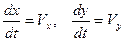

Вторая скобка согласно формуле (*) равна 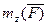, так как по основному закону динамики .

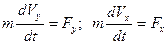Окончательно имеем

(28)

Полученное уравнение выражает теорему моментов относительно оси: производная по времени от момента количества движения точки относительно какой-нибудь оси равна моменту действующей силы относительно той же оси.

Из уравнения (28) следует, если 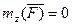, то .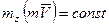

Теорема моментов относительно центра.

Ранее было показано, что

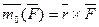
Аналогично

.

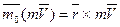При этом вектор 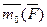направлен перпендикулярно плоскости, проходящей через центр О и вектор 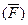, а вектор 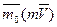- перпендикулярен плоскости, проходящей через центр О и вектор .

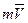Дифференцируем выражение 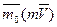по времени:

,

но 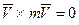, как вектор производной двух параллельных векторов, 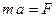. Следовательно

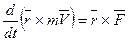
или

(29)

Теорема моментов.

Производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра.