Теорема об изменении количества движения точки.

Так как масса точки постоянна, а ее ускорение 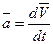, то уравнение (3) ( 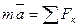), выражающий основной закон динамики, можно представить в виде:

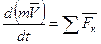(16)

Уравнение (16) выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме действующих на точку сил. Проинтегрируем это уравнение.

Пусть точка массы m, движущая под действием силы 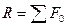имеет в момент t=0 скорость V₀, а в момент t₁ – скорость V₁. Умножим обе части равенства (16) на 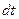и возьмем от них интегралы. При этом при интегрировании справа пределами будут 0 и t; а слева, где интегрируется, пределами интеграла будет соответствующие значения скорости V₀ и

Рис. 3.3

V₁. В результате получим:

.

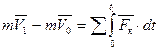Согласно формуле (14) окончательно имеем:

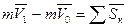(17)

Уравнение (17) выражает теорему об изменении количества движения точки: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот промежуток времени.

При решении задач вместо векторного уравнения (17) часто пользуются уравнениями в проекциях

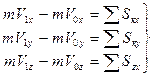(18)