Криволинейное движение точки.

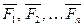Рассмотрим свободную материальную точку, движущуюся под действием сил . Проведем неподвижные координатные оси О х у z. Проектируя обе части равенства 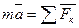на эти оси и учитывая, что и так далее получим дифференциальные уравнения криволинейного движения точки:

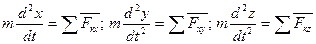(11)

Рис. 3.2

Так как действующие на точку силы могут зависеть от времени, от положения точки и от скорости, то по аналогии с (9) правые части уравнения (11) могут содержать время t, координаты точки х, у, z и проекции ее скорости 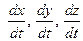. Уравнения (11) позволяют решать как первую, так и вторую (основную) задачу динамики. Чтобы с помощью этих уравнений решать основную задачу динамики, кроме действующих сил, надо знать начальные условия, то есть положение и скорость точки в начальный момент. В координатных осях О х у z начальные условия задаются в виде: при t = 0

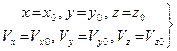(12)