Теорема об изменении кинетической энергии точки.

Рассмотрим точку массой m, перемещающуюся под действием приложенных к ней сил из положения М₀, где она имела скорость V₀ в положение М₁, где ее скорость V₁.

Основной закон динамики

.

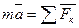Проектируем обе части равенства на касательную к траектории точки М, направленную в сторону движения получим:

.

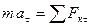Ускорение представим в виде

.

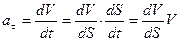В результате имеем:

.

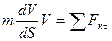Умножим обе части этого равенства на dS, внесем m под знак дифференциала.

Тогда замечая, что 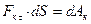, где 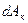- элементарная работа силы 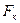, получаем выражение теоремы об изменении кинетической энергии в дифференциальной форме:

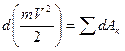(26)

Проинтегрировав обе части этого равенства в пределах соответствующих значений переменных в точках М₀ и М₁ получим

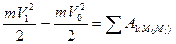(27)

Уравнение (27) выражает теорему об изменении кинетической энергии в конечном виде: изменении кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.