Вынужденные колебания. Резонанс. Рассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически изменяющаяся со временем сила
Рассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически изменяющаяся со временем сила 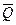 , проекция
, проекция  равна
равна
 (43)
(43)
Эта сила называется возмущающей силой, колебания, происходящие при действии такой силы, называются вынужденными. Величина p – называется частотой возмущающей силы.
Возмущающая сила может изменяться и по другому закону. Мы ограничимся, когда возмущающая сила изменяется по гармоническому закону.
Вынужденные колебания при отсутствии сопротивления
Дифференциальное уравнение движения имеет вид:
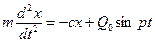
Разделим обе части на m и положим
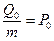 (44)
(44)
Тогда учитывая обозначения (30), приведем уравнение движения к виду:
 (45)
(45)
Уравнение (45) является дифференциальным уравнением вынужденных колебаний точки, при отсутствии сопротивления. Если решение состоит из общего и частного
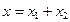
Полагая, что 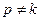 частные решения
частные решения 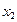 будем искать в виде:
будем искать в виде:
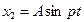 ,
,
Где А – постоянная величина, которую надо подобрать так, чтобы уравнение (45) обратилось в тождество. Подставляя 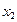 и
и  в уравнение(45) будем иметь
в уравнение(45) будем иметь



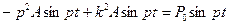
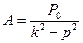
Таким образом, частное решение будет:
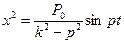 (46)
(46)
Общее решение уравнения (45) имеет вид:
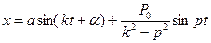 (47)
(47)
Где a и 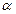 постоянные интегрирования
постоянные интегрирования
Решение (47) показывает, что колебания точки складывается из:
1. колебаний с амплитудой а (зависит от начальных условий) и частотой k, называемых собственными колебаниями;
2. колебаний с амплитудой А и частотой р, которые называются вынужденными колебаниями;
благодаря наличию тех или иных сопротивлений, собственные колебания будут довольно быстро затухать. Поэтому основным значением в рассматриваемом движении имеют вынужденные колебания, закон которых даётся уравнением (46).
Частота р вынужденных колебаний равна частоте возмущающее силы. Амплитуда этих колебаний, если разделить числитель и знаменатель 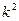 на, можно представить в виде:
на, можно представить в виде:
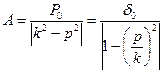 (48)
(48)
Где, согласно уравнения (30) и (44) 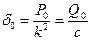 т.е.
т.е. 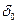 – величина статического отклонения точки под действием силы
– величина статического отклонения точки под действием силы 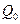 . Как видим, А зависит
. Как видим, А зависит
от отклонения 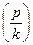 .
.
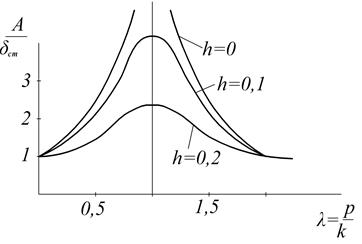
Рис. 3.13
h=0 при отсутствии сопротивления
1) При р=0 (или 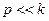 ) амплитуда равна
) амплитуда равна
2) При р=k амплитуда А становится очень большой
3) При  амплитуда А становится очень малой
амплитуда А становится очень малой
В случае, когда р=k, т.е. частота возмущённой силы равна частоте собственных колебаний, имеет место так называемое явление резонанса.
Дата добавления: 2015-06-17; просмотров: 1004;
