Дифференциальные уравнения движения системы.

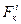Рассмотрим систему, состоящую из «n» материальных точек. Выделим какую-нибудь точку системы с массой m_к. Обозначим равнодействующие всех приложенных к точке внешних сил через , а равнодействующие всех внутренних сил - . Если точка имеет при этом ускорение 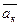, то по основному закону динамики

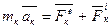(2)

Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

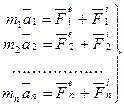(3)

Эти уравнения, из которых можно определить закон движения каждой точки системы, называется дифференциальными уравнениями движения системы в векторной форме. Уравнения (3) являются дифференциальными, так как 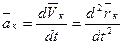. Полное решение основной задачи динамики для системы состояла бы в том, чтобы, зная заданные силы, проинтегрировать соответственные дифференциальные уравнения и определить закон движения каждой из точек системы в отдельности.

Однако такой путь обычно не применяют по двум причинам. Во-первых, слишком сложен математически. Во-вторых, в большинстве случаев при решении задач механики бывает достаточно знать некоторые суммарные характеристики движения системы в целом, а не движения каждой из ее точек. Эти суммарные характеристики определяются с помощью общих теорем динамики.