Теорема о движении центра масс.

Сложим почленно левые и правые части уравнения (3).

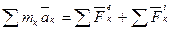(4)

Преобразуем левую часть. Из формулы (1^/) имеем

Дважды продифференцируем

или

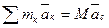, (5)

где 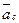- ускорение центра масс системы.

Так как по свойству внутренних сил системы 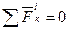, то подставляя все найденные значения в равенство (4) получим:

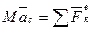(6)

Уравнение (6) и выражает теорему о движении центра масс системы. Данная теорема может быть сформулирована: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Проектируя обе части равенства (6) на оси координат, получим:

(6^/)

Значение теоремы состоит в следующем:

1). Из уравнения (5^/) видно, что решения, которые мы получим, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела.

2). Теорема позволяет при определении закона движения центра масс любой системы исключить из рассмотрения все наперед неизвестные внутренние силы.