Закон сохранения движения центра масс.

Из теоремы о движении центра масс можно получить важные следствия.

1). Пусть сумма внешних сил, действующая на систему, равна нулю

.

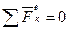Тогда из уравнения (6) следует, что 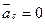или .

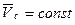Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, то есть равномерно и прямолинейно.

2). Пусть сумма внешних сил не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например ось О_х) равна нулю: .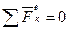

Тогда первое из уравнений (6^/) дает:

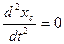или .

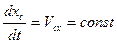Следовательно, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная.

В частности, если в настоящий момент , то в любой последующий момент , то есть центр масс системы вдоль оси х перемещаться не будет.

Пример.

Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий не мог двигаться вдоль горизонтальной плоскости, так как в этом случае сумма проекций на горизонтальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет ( ).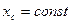

Если человек вынесет правую ногу, то левая его нога скользнет назад, а общий центр масс останется на месте.

При наличии трения скольжению левой ноги назад будет препятствовать сила трения, которая в этом случае будет направлена вперед. Эта сила и будет внешней силой, которая позволяет человеку перемещаться вперед.

Аналогично движение автомобиля.

Сила давления газа в двигателе является внутренней силой. Двигатель передает вращающий момент. При этом точка В стремиться скользнуть влево. Тогда на колесо будет действовать сила трения направленная вправо. Эта внешняя сила и позволит центру тяжести машины двигаться вперед.

Рис. 4.2