Теорема об изменении количества движения.
Рассмотрим систему, состоящую из «n» материальных точек, составим для этой системы дифференциальные уравнения движения (2) и сложим их почленно
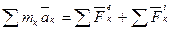 .
.
Последняя сумма по свойству внутренних сил равна нулю. Кроме того,
 .
.
Окончательно находим
 (9)
(9)
Уравнение (9) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.
В проекциях на координате оси будем иметь:
 (10)
(10)
Найдем другое выражение теоремы. Пусть в момент t=0 количество движения равно  , а в момент t1 становится
, а в момент t1 становится  . Тогда, умножая обе части равенства (9) на dt и интегрируя, получим:
. Тогда, умножая обе части равенства (9) на dt и интегрируя, получим:
 или
или
 (11)
(11)
Уравнение (11) выражает теорему об изменении количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
В проекциях на координатные оси:
 (12)
(12)
Дата добавления: 2015-06-17; просмотров: 691;
