Момент инерции тела относительно оси.
Положение центра масс характеризует распределение масс системы не полностью.

Если расстояние h от оси z увеличить на одну и ту же величину, то положение центра масс не изменить, а распределение масс станет другим, и это скажется на движении системы. Поэтому в механике вводится еще одна характеристика – момент
Рис. 4.5 инерции. Моментом инерции тела (системы) относительно данной оси Оz (осевым моментом инерции) называется скалярная величина
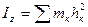
Осевой момент играет при вращательном движении такую же роль, какую масса при поступательном , то есть осевой момент инерции является мерой инертности тела при вращательном движении.
Момент инерции относительно параллельных осей (Теорема Гюйгенса)
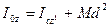 , где
, где
с – центр масс,
О – произвольная точка.
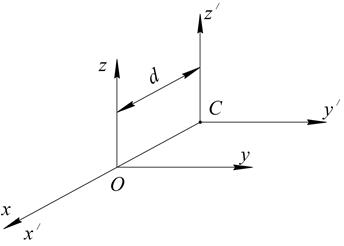
Рис. 4.6
Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс, сложенному с произведением массы всего тела на квадрат расстояния между осями.
Центробежные моменты инерции.
Момент инерции относительно оси также не характеризует распределение масс системы полностью. Например, если стержень ДЕ на рисунке 4.5 повернуть в плоскости оуz так, чтобы угол между ним и осью Оz не был прямым, а расстояние h шаров А и Б от оси сохранить, то распределение масс станет другим (симметрия относительно оси Оz нарушится) и это скажется при вращении системы вокруг оси Оz (возникнут боковые давления на подшипники). Поэтому в механике в качестве характеристик, учитывающих подобную асимметрию, вводят так называемые центробежные моменты инерции.
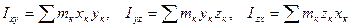 , где
, где
mк – массы точек, хк, ук, zк – координаты точек, могут быть и положительные и отрицательные, а также обращенные в нуль.
Часто в ходе расчетов пользуемся понятием радиуса инерции. Радиусом инерции относительно оси Оz называется линейная величина 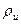 определяется равенством
определяется равенством 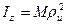 .
.
Момент инерции некоторых однородных тел.
1. Тонкий однородный стержень

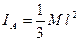
2. Тонкое круглое однородное кольцо

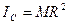
Круглая однородная пластина или цилиндр радиуса R и М


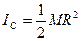
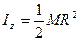
Дата добавления: 2015-06-17; просмотров: 1075;
