Главный момент количества движения системы.

Главным моментом количества движения (или кинематическим моментом) системы относительно данного центра О называется величина К₀, равная геометрической сумме моментов количества движения всех точек системы относительно этого центра:

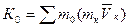(13)

Аналогично определяются моменты количества движения системы относительно осей координат:

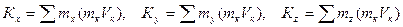(14)

Подобно тому, как количество движения системы является характеристикой ее поступательного движения, главный момент количества движения системы является характеристикой вращательного движения системы.

Определение вектора К₀ сводится к определению его проекций К_x, К_y, К_z.

Найдем сначала для К_z ; то есть кинетический момент вращательного тела относительно оси вращения.

Для любой точки, отстоящей от оси вращения на расстояние h_к, скорость 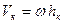. Следовательно, для этой точки 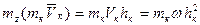. Тогда для всего тела

,

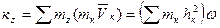где 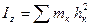- момент инерции тела относительно оси z.

Окончательно находим

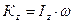(15)

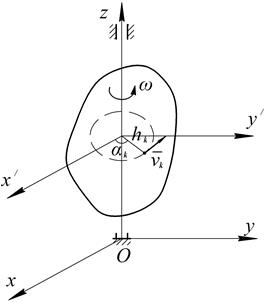
Рис. 4.7

Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то очевидно

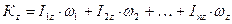(16)

Вычислим теперь величины к_x, к_y. Для определения 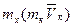, необходимо спроектировать вектор 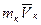на плоскость Оyz, то есть на ось у^/.

Получим .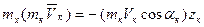

Но 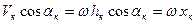, в результате получим

,

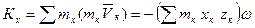где I x z - центральный момент, таким образом

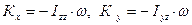(17)