Кинетическая энергия системы.

Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы.

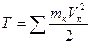(20)

Кинетическая энергия является характеристикой и поступательного и вращательного движения системы. Кинетическая энергия является скалярной величиной и при том положительной. Она зависит от направлений движений и не характеризует изменений этих направлений. На изменение кинетической энергии влияет действие внешних и внутренних сил.

Если система состоит из нескольких тел, то ее

.

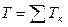Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. Следовательно, для любой точки V_к = V_с и формула(19) дает

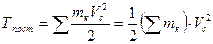или

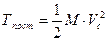, (21)

где М – масса тела,

V_с – скорость центра масс.

Вращательное движение.

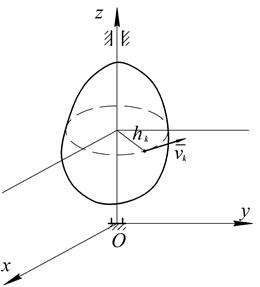
Рис. 4.8

,

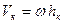где h_к – расстояние точки от оси вращения,

- угловая скорость.

Подставляя в (17), получим:

.

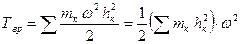
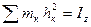(22)

Плоскопараллельное движение.

При этом движении скорости всех точек в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р. Следовательно по формуле (21)

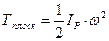(23)

I_Р – момент инерции относительно названной оси,

- угловая скорость тела.

Величина I_Р – будет переменной, так как положение центра Р при движении тела все время меняется. Введем вместо I_Р постоянный момент инерции I_с, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса 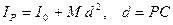. Подставим I_Р в (19^/).

Рис. 4.9 Учитывая, что точка Р – мгновенный центр скоростей и следовательно 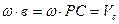, где V_с – скорость центра масс С. Окончательно:

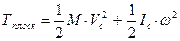(24)

Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.

Общий случай движения.

Если за полюс взять центр масс С тела, то движение тела в общем случае будут слагаться из поступательного движения со скоростью V_с и из вращения вокруг мгновенной оси СР, проходящей через этот полюс. Тогда скорость в любой точке ,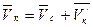

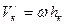, h_к – расстояние точки от оси СР, - абсолютная угловая скорость.

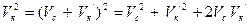
Рис. 4.10 и учитывая, что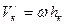

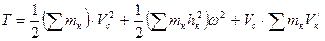
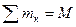- масса тела,

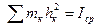- момент инерции относительно мгновенной оси,

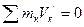, так как она представляет количество движения, получаемое телом при его вращении вокруг оси ОР, проходящей через центр масс тела.

Окончательно получаем:

(25)

Кинетическая энергия равна кинетической энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг оси, проходящей через центр масс.