Потенциальное силовое поле и силовая функция.
Работа на перемещение 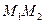 силы F приложенной в точке
силы F приложенной в точке 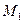 вычисляется по формуле
вычисляется по формуле
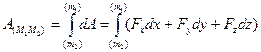 (33)
(33)
Вычислить данный интеграл, не зная происходящего движения (то есть зависимостей x, y,z от времени t) можно лишь в случае, когда сила зависит только от положения точки, то есть её координат x, y,z. Про такие силы говорят, что они образуют силовое поле. Силовым полем называется часть пространства, в каждой точке которого на помещённую материальную частицу действует определённая по модулю и направлению сила, зависящая от положения частицы. Примером силового поля служит поле тяготения планеты или Солнца.
Так как, сила определяющая её проекции на оси координат то силовое поле задаётся уравнениями:
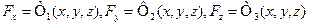 (34)
(34)
Однако, если окажется что выражение стоящее в формуле (1) под знаком интеграла и представляющее собой элементарную работу силы, будет полным дифференциалом некоторой функции 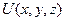 т.е. будет
т.е. будет
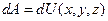 или
или 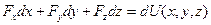 (35)
(35)
Функция, 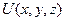 дифференциал которой равен элементарной работе, называется силовой функцией. Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле – потенциальными силами. Если в формулу (33) подставить из равенства выражения из равенства (35) то будем иметь:
дифференциал которой равен элементарной работе, называется силовой функцией. Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле – потенциальными силами. Если в формулу (33) подставить из равенства выражения из равенства (35) то будем иметь:
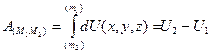 (36)
(36)
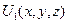 ,
, 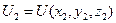 – значение силовой функции в точках
– значение силовой функции в точках 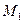 и
и 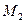 . Следовательно, работа поступательной силы равна разности значений силовой функции в конечной и начальных точках пути, и от вида траектории движущейся точки не зависит.
. Следовательно, работа поступательной силы равна разности значений силовой функции в конечной и начальных точках пути, и от вида траектории движущейся точки не зависит.
Силы, работа которых зависит от вида траектории или от закона движения точки приложенной силы – не потенциальным (сила трения и сопротивления среды).
Примером потенциальных сил являются сила тяжести, упругая сила и сила тяготения.
– для силы тяжести, если ось z верх
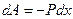 , считая
, считая 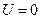 при
при 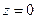 находим
находим 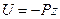
– для упругой силы, действующей вдоль оси Ox 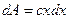 , считая
, считая 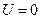 при
при 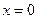 находим:
находим: 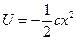
– для силы тяготения
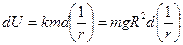 откуда считая
откуда считая 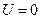 при
при 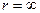
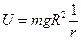
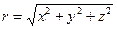
Дата добавления: 2015-06-17; просмотров: 1708;
