Теорема об изменении кинетической энергии системы.

Показанная в п. 3.5. теорема справедлива для любой точки системы. Следовательно, если рассмотреть какую-нибудь точку системы с массой m_к имеющую скорость V_к, то для этой точки будет

,

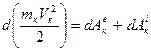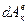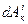где и – элементарная работа действующих на точку внешних и внутренних сил. Составляя, такие уравнения для каждой из точек системы и складывая их почленно, получим

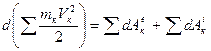
или

(29)

Равенство (29) выражает теорему об изменении кинетической энергии системы в дифференциальной форме.

Проинтегрировав обе части этого равенства в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна Т₀, в положение, где значение кинетической энергии становится равным Т₁ будет иметь

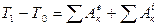(30)

Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

Рассмотрим два важных частных случая.

1). Неизменная система. Неизменной будем называть систему, в которой расстояния между точками приложения внутренних сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

Пусть две точки В₁ и В₂ действуют друг на друга с силам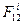и и 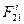( 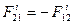), имеют в данный момент скорости V₁ и V₂. Тогда за промежуток времени dt эти точки совершат элементарные перемещения 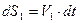и 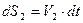. Но так как отрезок В₁ В₂ является неизменным, то по известной теореме кинематики проекции векторов 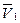и 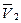, а следовательно, и перемещений и на направление отрезка В₁ В₂ будут равны друг другу, то есть . Тогда элементарные работы 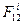и 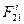будут одинаковы по модулю и противоположны по знаку и в сумме дадут нуль. Этот результат справедлив для всех точек.

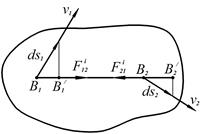
Рис. 4.13

Отсюда заключаем: Для неизменной системы сумма работ всех внутренних сил равна нулю и уравнения (29) (30) принимают вид

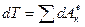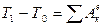или (31)

2). Система с идеальными связями.

Рассмотрим систему, на которую наложены связи, не изменяющие со временем.

Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда уравнение (29) можно представить в виде

,

где 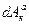– элементарная работа, действующая на каждую точку систему внешних и внутренних активных сил,

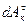– элементарная работа реакции наложенных на ту же точку внешних и внутренних сил.

Можно ввести понятие о таких «идеальных» механических системах, у которых наличие связей не влияет на изменение кинетической энергии системы при ее движении. Для таких связей должно, очевидно, выполнено условие:

.

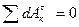Если для связей, не изменяющихся со временем, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи называются идеальными.

Укажем некоторые виды таких связей:

– неподвижная поверхность, трением о которую можно пренебречь, то при скольжении тел вдоль такой поверхности работа реакции N равна нулю.

– качение без скольжения тела по шероховатой поверхности работа нормальной силы N и силы трения F (то есть касательная составляющая реакции) равна нулю.

– работа реакции R шарнира, если пренебречь трением, будет равна нулю, поскольку точка приложения силы R при любом перемещении систем остается неподвижной.

– если материальные точки В₁ и В₂ (§5.3.) рассматривать как связанные жестким (нерастяжимым) стержнем В₁ В₂ , то силы 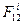и 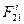будут реакциям стержня; работа каждой из этих реакций не равна нулю, но сумма этих работ дает нуль.

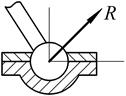
Рис. 4.14

Для механической системы, на которую наложены идеальные связи, будем очевидно иметь

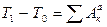или (32)

Таким образом, изменение кинетической энергии системы с идеальными связями при любом ее перемещении равно сумме работ на этом перемещении, приложенных к системе внешних и внутренних активных сил.