Вынужденные колебания в последовательном контуре.
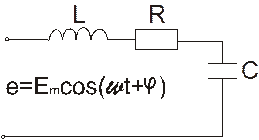
Итак, контур подключен теперь к источнику высшей гармонической электродвижущей силы с амплитудой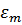 
.
Составим дифференцированное уравнение колебания:
2 – е уравнение Кирхгофа: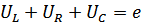 
, где 
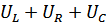– падение напряжения на каждом участке , 
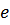- мгновенное ЭДС.
+ 
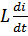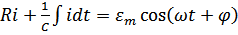
Для упрощения нахождения амплитуд и начальных фаз вынужденных колебаний воспользуемся приемом, получившие название метода комплексных амплитуд. Он необходим для анализа линейных систем и для нахождения линейных величин.
Этот метод основан на связи функций тригонометрических и экспоненциальных (на формулах Эйлера).
Эти формулы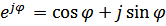 
; 
.
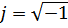Эти формулы нужны для замены тригонометрических функций показательными.
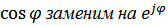и проведем все вычисления в экспоненциальной форме.
Мы получаем ответ в виде комплексного числа и мнимая часть отбрасывается.
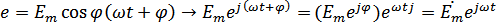
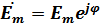– комплексная амплитуда ЭДС.
Комплексная амплитуда характеризует амплитуду и начальную фазу сигнала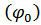 
.
Теперь уравнение имеет вид:
( 
)
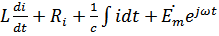Частное решение также будет иметь комплексный вид: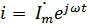 
Интегрируемая только частным решением, общее решение быстро затухает.
Подставим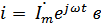 
( )
= 
= 
( 
)
= 
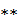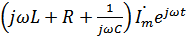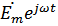
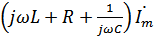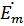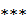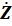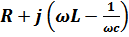– импеданс цепи (полное сопротивление)
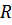– активное сопротивление цепи
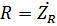– импеданс активного сопротивления.
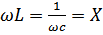– реактивное сопротивление цепи (контура),
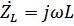– импеданс катушки,
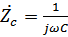- импеданс конденсатора,
, 
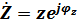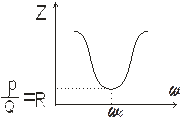
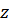– модуль полного сопротивления цепи,
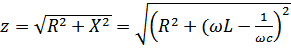– модуль 
.
( 
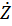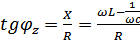) или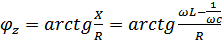 
– аргумент 
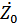(комплексного числа).
Решаем уравнение ( )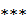 
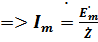– комплексная форма.
; 
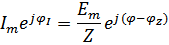
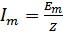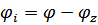(где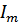 
- амплитуда тока, 
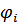- фаза тока)
Преобразуем: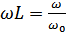 
; 
( 
; 
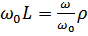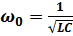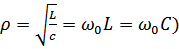
Подставим в уравнение для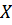 
:
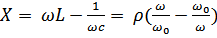, где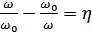 
- обобщенная расстройка.
,
,
, 
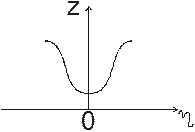
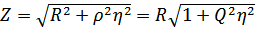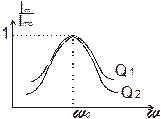
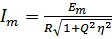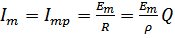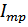- резонансная.
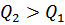
Амплитуда колебаний при резонансе пропорциональна добротности.
Определение добротности (как определить добротность)
Имеем: 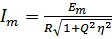, учитывая 
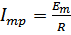получим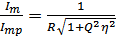 
Пусть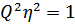 
, тогда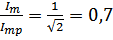 
.
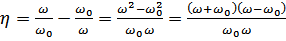Считаем, что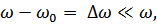 
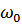- очень мало
Тогда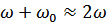 
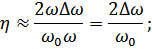
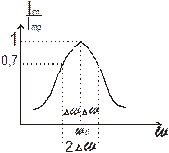
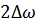– ширина полосы пропускания контура.
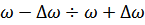- полоса пропускания контура.
; 
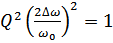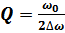– т.о. определяется добротность.
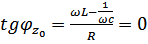– при резонансе.
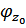- аргумент 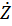- комплексные числа. (Ток и напряжение совпадают при резонансе).
Графики вышеприведенных зависимостей показывают, что последовательный контур является фильтром, обеспечивающим передачу сигналов, частоты которых находятся в окрестности резонансной частоты.
Дата добавления: 2015-06-22; просмотров: 1679;