Линейный четырехполюсник

Под линейным четырехполюсником понимают устройство с четырьмя зажимами, двумя входными и двумя выходными.

Задача любой линейной цепи является обеспечение функций передачи и фильтрации сигналов в тракте канала связи.

Обозначается:

Пусть на вход подаем -й сигнал. На выходе будет такой же -й сигнал, но может измениться амплитуда с фазой.

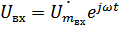
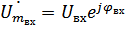
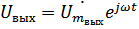
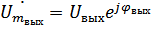
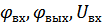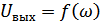, - все они функции частоты.

Чем характеризуются 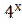полюсники:

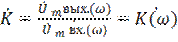-комплексный коэффициент передачи 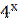полюсника зависит от частоты ( )

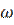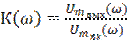- Амплитудно-частотная характеристика 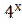полюсных. (АЧХ)

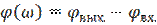-фазочастотная характеристика 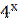полюсника. (ФЧХ)

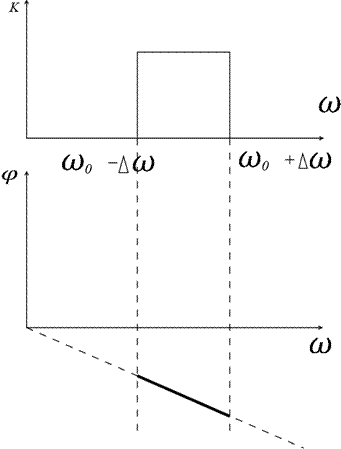
· Какими должны быть характеристики 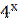полюсника, чтобы он не искажал сигнал?

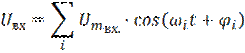
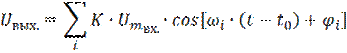
K=K(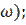

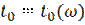
· Чтобы сигнал не искажался, необходимо чтобы в некотором диапазоне частот ( ширина канала связи) коэффициент передачи 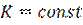был бы постоянным, а время задержки 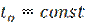не зависело бы от частоты.

·

;

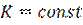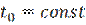
Это идеальные характеристики.

Насколько реальные близки к идеальным опред. Допустимыми источниками.

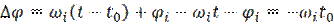
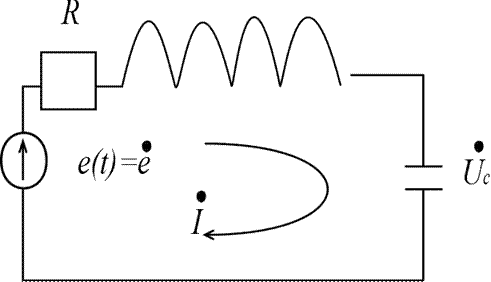
Фильтрующие свойства последовательного контура.

-пример линейного 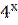полюсника, который можно использовать в качестве фильтра.

Найдем коэффициент передачи для этой системы, равный отношению комплексной амплитуде напряжения на конденсаторы Аmc к комплексной амплитуде ЭДС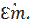

;

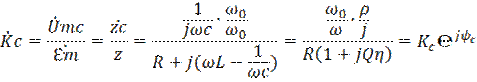
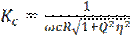Если снимать сигнал с катушки: Если снимать сигнал с :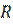

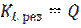
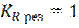
При резонансе амплитуда колебаний на катушке и конденсаторе увеличивается в 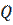раз.

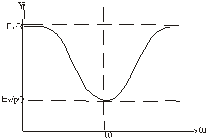
в близи собственной частоты эта характеристика близка к идеальной.

Фазачастотная характеристика – линейна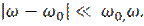

Рассмотренный случай является примером фильтра.

Фильтры служат для разделения токов различных частот, т.е. одни частоты несут информацию, а другие оказывают вредное воздействие.

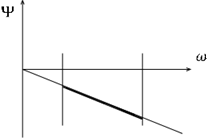
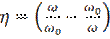-обобщенная расстройка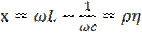

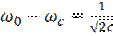резонансная частота контура

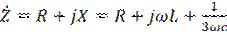- полное сопротивление последовательного контура

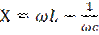реакт. сопротивление контура

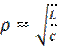– характеристическое сопротивление контура

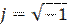
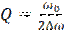– добротность

2 - ширина полосы пропускания.

; ;

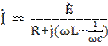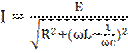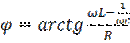
Напряжение на инд-ти и емкости:

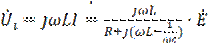
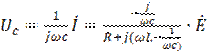
При частоте 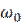- резонансной выражение в скобках обратится в нуль, т.е. при 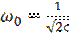, ток в цепи достаточно меньшего значения: 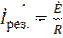при этом напряжение на L и C соответствует:

;

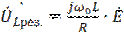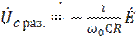
Величина называющая во сколько раз при резонансе амплитуда этих превышает амплитуду ЭДС генераторе называется добротностью 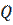- затухание.

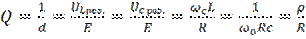, где 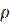-характеризуется сопротивлением контура.

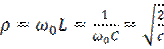
Классификация фильтров

Фильтры классифицируются по признаку частот, пропускаемых в исследуемую цепь.

I. Фильтры Низких Частот- ФНЧ

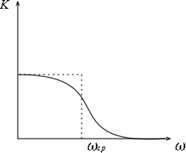
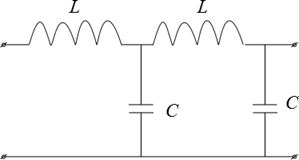
II. Фильтры Высоких Частот- ФВЧ

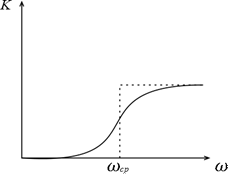
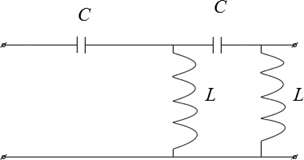
III. Полосовой фильтр –пропускает частоты в некоторой полосе (ПФ)

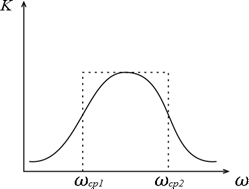Пример полосового фильтра – последовательный контур

IV. Заградительный фильтр – пропускает все частоты, кроме некоторой полосы. (ЗФ)

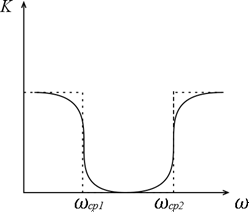
Полосовой Фильтр можно получить как фильтр высоких частот с 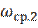плюс фильтр низких частот с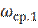

ПФ= ФВ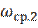Ч +ФНЧ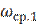

Фильтр наиболее полно характеризуется зависимостью коэффициента передачи от частоты. Коэффициент передачи мощности сигнала на выходе фильтра и мощности поступающей на вход, удобно оценивать в логарифмической шкале. За единицу отношения мощности принят бел( в честь А.Г. Белла), которая определяется как

,

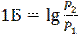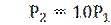
На практике используются, как правило, (величина в 10 раз меньше) децибелом, 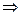коэффициент передачи, выраженный в децибелах:

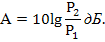
Из-за квадратичной зависимости мощности тока (напряжения) коэффициент передачи тока (напряжения) определяется как: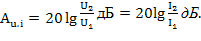

Октава - изменение частоты вдвое.

Декада- изменение частоты в 10 раз.

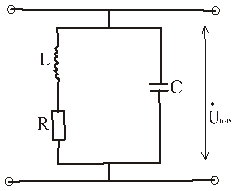
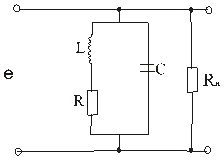
Параллельный контур

Здесь R_i – омическое сопротивление витков катушки.

Комплексное сопротивление цепи: 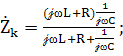причем ωL 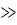R.

В числителе " R" - мы можем пренебречь, а в знаменателе R нельзя пренебречь, так как знаменатель может превратиться в 0 при ω=ω₀.

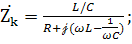
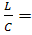квадрат характеристического сопротивления.

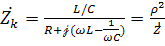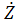; - полное сопротивление ( 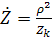; ρ= )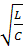

;

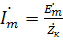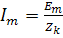
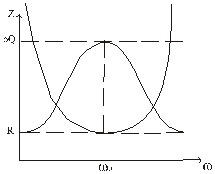
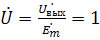
Влияние сопротивления генератора и нагрузки на свойства параллельного контура

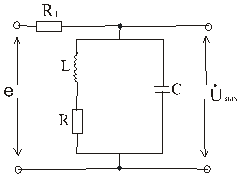R_г- сопротивление генератора

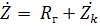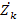( - сопротивления контура, 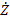– общее сопротивление)

Амплитуда: 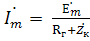; (= 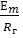- контур на ток не влияет)

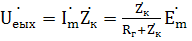
Коэффициент передачи: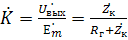

Рассмотрим 2 случая

1. 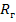- очень мало, т.к.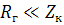

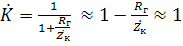. Тогда резонансные свойства контура практически не проявляются

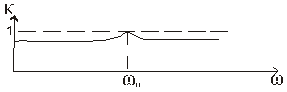
2. ;

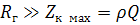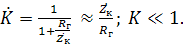
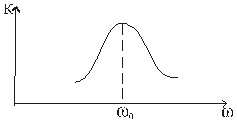
Влияние сопротивления нагрузки

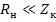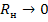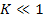1. , если , то т. к. 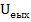очень мало.

2. 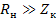- нагрузка не влияет на свойства контура. И сопротивление генератора и сопротивление нагрузки должно быть большим, в этом случае проявляются резонансные свойства контура.

Влияние сопротивлений генератора и нагрузки на свойства последовательного контура

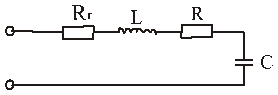
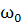- собственная частота

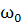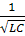= – не меняется

ρ = 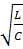(характеристическое сопротивление) не изменяется

Q= →добротность уменьшается

Как влияет 𝑅 нагрузки:

1) 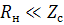, 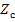- сопротивление конденсатора 𝐾 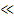1, 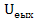- мало

2) 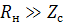нагрузка не влияет на свойства контура

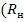-входное сопротивление)

- должно быть как можно больше, 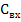- как можно меньше.

Прохождение модулированных колебаний через контур- фильтр

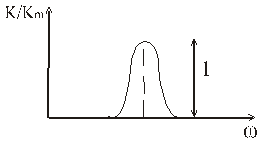
Чтобы получить спектр выходного сигнала необходимо умножить спектр входного сигнала на амплитудно- частотную характеристику (𝑈=𝑈(ω))

1. 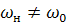, умножаем графически

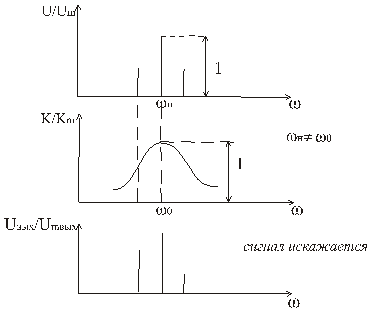
2. 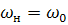Собственная частота сигнала = несущей частоте контура. (т.е. контур сделали качественным)

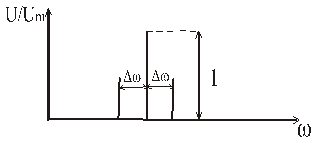
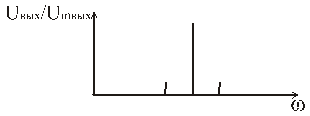
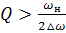
m - коэффициент модуляции, уменьшается

Сигнал искажается

3. 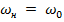(собственная частота контура = несущей частоте сигнала)

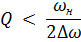
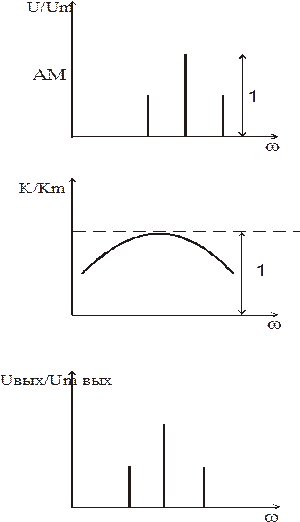
Искажения информации минимальны

Для согласования фильтра и сигнала необходимо, чтобы:

1. 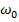(собственная частота) фильтра совпадала с несущей частотой сигнала;

2. Ширина полосы фильтра была бы не меньше ширины полосы сигнала.

Связанные контуры

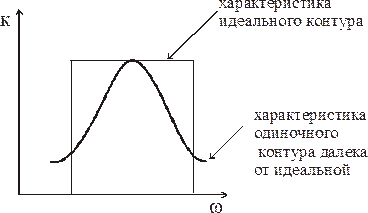
Идеальный фильтр должен иметь П-образную частотную характеристику и линейную фазовою характеристику в полосе пропускания. Для приближения частотной характеристики к идеальной используется система нескольких контуров, связанных между собой либо общим магнитным полем (индуктивная связь), либо общим электрическим полем (емкостная связь).

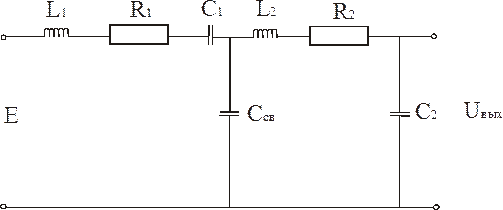
Общий элемент 2-х контуров -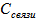

Такая связь называется - емкостной.

Связь может быть индуктивной, гальванической , когда общий элемент - резистор.

Связь может быть сложной, когда общий элемент - какие-то схемы.

Вид связи всегда относителен.

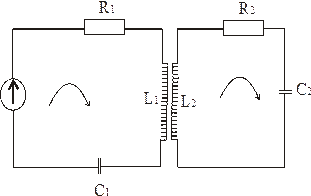
Рассмотрим трансформаторную связь (индуктивную).

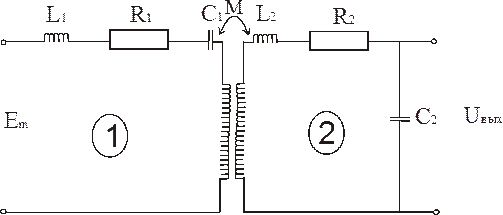
М - коэффициент взаимоиндукции.

ЭДС: 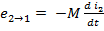- ЭДС, вносимая из 2-ого контура в 1

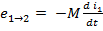- ЭДС, вносимая из 1-ого контура во 2-ой

Представим токи в виде: ( 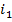и )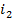

(*)

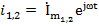(Система уравнений Кирхгофа)

Запишем уравнение в комплексных амплитудах

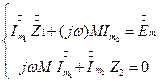Система уравнений с 2 неизвестными

Решив систему окажется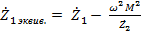

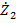- сопротивление, вносимое из контура 2 в контур 1.

Пусть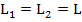

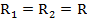
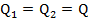- добротность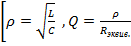

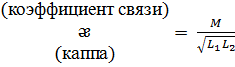- коэффициент связи.

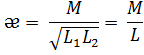
Свойства схемы определяются величиной æ Q

Рассмотрим случаи:

1. æ Q <<1 - случай слабой связи.

Обозначим - коэффициент передачи одиночного контура, тогда максимальный коэффициент передачи будет равен:

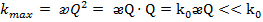
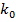= Q - при резонансе

В этом случае амплитудно-частотная характеристика имеет вид:

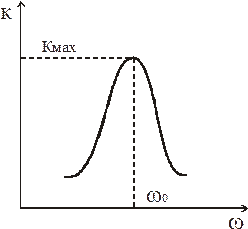
— полоса уже, чем для одиночного контура

2. æ Q =1 - случай критической связи

коэффициент передачи: 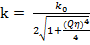; η = 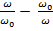— обобщенная расcтройка

при резонансе η= 0, тогда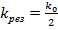

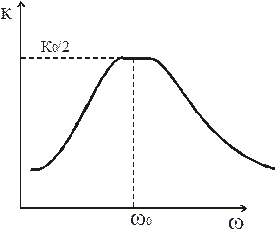
Амплитудно-Частотная Характеристика ближе к П-образной.

3. æ Q >1 Случай сильной связи

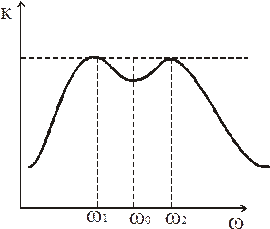
Появляются 2 резонансные частоты

У каждого из одиночных контуров собственная частота - 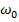, а когда их связывают, при сильной связи, у них появляется 2 собственные частоты 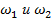- при сильной связи частота расходится на 2-е.

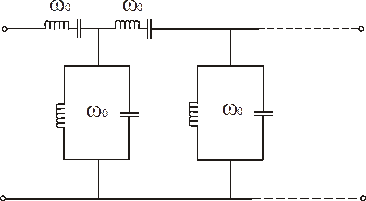
Схемы сложных фильтров :

Полосовой фильтр:

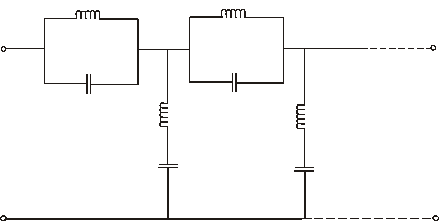
Заградительный фильтр:

Линейные цепи с распределенными параметрами

Если длина двухпроводной линии больше длины волны распространяющегося в ней сигнала ( 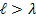), то ток в данный момент времени неодинаков в различных сечениях линии , и линия называется поэтому цепью с распределенными постоянными ([Этими постоянными (или параметрами линии) являются отнесенные к единице длины емкость проводов C , индуктивность L, сопротивление R и проводимость материала изоляции между проводами 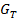][Линия называется однородной , если эти параметры одинаковы в любом участке]).

Итак, распределенность параметров нужно учитывать на высоких частотах: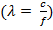

Элементы, в которых надо учитывать распределение параметров называются длинными линиями.

Излучение таких проводов очень мало.

Все электромагнитное поле сосредоточено между проводами

.

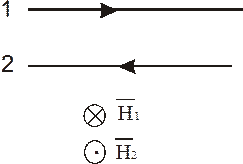
Характеристика длинных линий

В данной линии каждый элемент 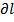характеризуется индуктивностью 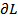, емкостью 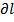, активными сопротивлениями , проводимостью .

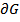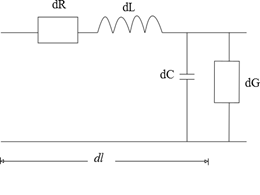
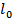-индуктивность на единицу длины (погонная индуктивность)

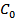-погонная емкость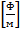

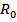-погонное сопротивление

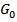-погонная проводимость

Длинные волны подчиняются (описываются)

Телеграфными уравнениями

(для линии без потерь)

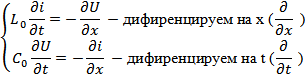
(с потерями)

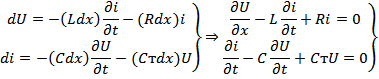
Решая систему т. е. дифф. 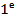уравнение по x, второе по tи исключим из первого уравнения ток, и исключим из второго напряжение и вводя обозначения 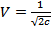, получим:

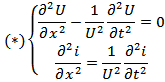
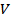-Скорость распространения сигнала в длинной линии

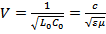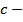; скорость света в вакууме, 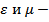относительная диэл-кая и магнитная проницаемость среды.