Линейный вращающийся трансформатор (ЛВТ).

Для получения линейной зависимости выходного напряжения от угла поворота ротора α необходимо, чтобы это напряжение определялось уравнением

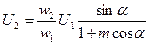, (3.96)

где m – величина постоянная, определяемая магнитными и электрическими параметрами ЛВТ.

При m ≈ 0,54 зависимость (3.96) получается линейной с точностью до 1% в пределах изменения угла поворота 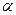от 0° до 60° (рис. 3.62). Для получения указанной зависимости 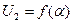применяют следующую схему включения обмоток ЛВТ: синусную обмотку соединяют последовательно с компенсационной обмоткой, а косинусную обмотку замыкают на некоторое неизменное сопротивление Z_C (рис. 3.63). При этом величина сопротивления Z_C выбирается такой, чтобы обеспечить полное вторичное симметрирование обмоток при заданной нагрузке Z_H.

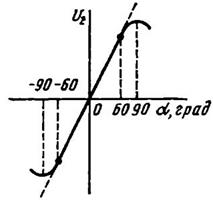
Рис. 3.62. Зависимость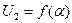

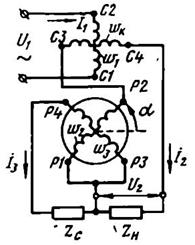
Рис. 3.63. ЛВТ со вторичным симметрированием

Для определения требуемой величины Z_C можно воспользоваться уравнением:

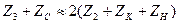(3.97)

Иными словами, для полного вторичного симметрирования обмоток необходимо, чтобы полное сопротивление цепи косинусной обмотки было равно удвоенному полному сопротивлению цепи синусной обмотки (включая сопротивления компенсационной обмотки Z_К и нагрузки Z_H).

Однако полное вторичное симметрирование обмоток возможно лишь при неизменной нагрузке ЛВТ (Z_H = const). В случае переменной нагрузки ЛВТ применяется схема первичного симметрирования обмоток (рис. 3.64), в которой обмотка возбуждения включается последовательно с косинусной обмоткой и сопротивлением Z_C, а компенсационная обмотка замыкается на некоторое сопротивление Z_HК. Сопротивления Z_C и Z_HК выбираются такими, чтобы магнитный поток компенсационной обмотки Ф_К и поперечный поток косинусной обмотки 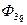, были взаимно скомпенсированы при любом значении угла .

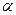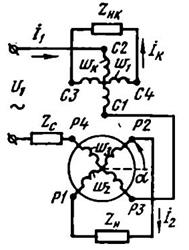
Рис. 3.64. Принципиальная схема ЛВТ с первичным симметрированием