Свободные колебания в контуре
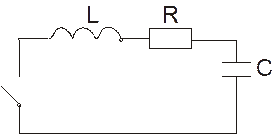
Анализ линейных цепей основан на свойствах линейных уравнений и связях тригонометрических и показательных функций.
В момент времени 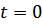 ,
, 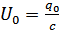 . Составим дифференцированное уравнение для этой цепи.
. Составим дифференцированное уравнение для этой цепи.
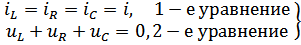 – 2-ой закон Кирхгофа для этой цепи.
– 2-ой закон Кирхгофа для этой цепи.
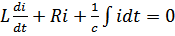 ; учитывая, что
; учитывая, что 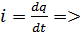 то
то
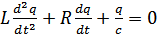
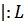
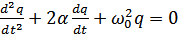 , где
, где 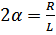 ;
; 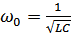
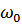 – собственная частота контура,
– собственная частота контура,
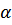 - коэффициент затухания.
- коэффициент затухания.
Рассмотрим случай 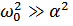 (
( 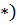 (наиболее интересен для радиотехники).
(наиболее интересен для радиотехники).
Решением уравнения 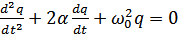 будет:
будет:
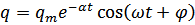
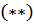 , где
, где 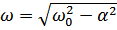 , т.е. зависимость заряда на конденсаторе от времени имеет характер затухающего колебания, частота которого, называемая частотой свободных колебаний, несколько меньше собственной частоты контура
, т.е. зависимость заряда на конденсаторе от времени имеет характер затухающего колебания, частота которого, называемая частотой свободных колебаний, несколько меньше собственной частоты контура 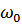 .
.
Из начальных условий определим 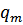 и
и 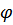 :
:
Начальные условия:
1. 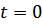
2. 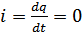
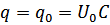 , при
, при 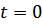 ,
, 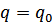 ,
, 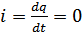 ,
, 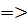
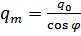 ,
, 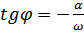 .
.
Откуда (из (2)) получим:
Из решения уравнения (2) продифференцируем его при условии 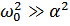 получим, что
получим, что 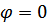 .
.
Из 1-го начального условия: 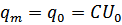
Тогда решение уравнения запишем в виде (т.о. ( 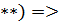 )
)
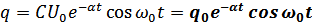 .
.
Т.к. 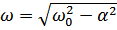 , с учетом (
, с учетом ( 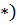
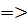
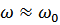 (
( 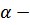 коэффициент затухания).
коэффициент затухания).
Условие ( 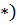 означает, что затухание мало.
означает, что затухание мало.
Закон изменения силы тока находим, дифференцируя 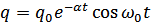 по времени:
по времени:
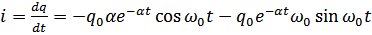 (т.к.
(т.к. 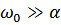 , то первым слагаемым пренебрегаем)
, то первым слагаемым пренебрегаем) 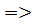
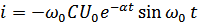 (т.к.
(т.к. 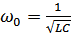 то)
то)
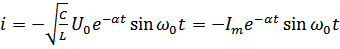 , где
, где 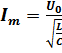 – амплитуда тока.
– амплитуда тока.
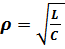 - называется характеристическим сопротивлением контура, равное отношению амплитуды напряжения на конденсаторе к амплитуде силы тока.
- называется характеристическим сопротивлением контура, равное отношению амплитуды напряжения на конденсаторе к амплитуде силы тока.
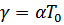 , где
, где 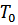 – период собственных колебаний.
– период собственных колебаний.
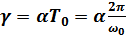 – декремент затухания.
– декремент затухания.
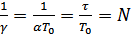 – количество периодов, за которое амплитуда уменьшается в
– количество периодов, за которое амплитуда уменьшается в 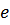 раз.
раз.
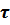 – время, за которое амплитуда изменяется в
– время, за которое амплитуда изменяется в 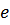 раз.
раз.
Относительную убыль энергии в процессе колебания характеризует добротность 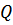 .
.
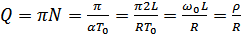
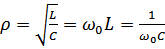 ,
, 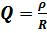 – добротность.
– добротность.
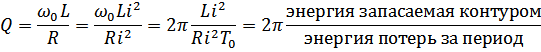
(с помощью 3-х параметров 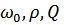 – можно описать колебания в любой системе).
– можно описать колебания в любой системе).
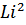 - энергия запасаемая контуром
- энергия запасаемая контуром
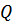 - характеризует потери
- характеризует потери
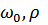 - характеризуют собственные колебания
- характеризуют собственные колебания
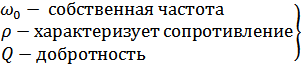 При их помощи можно описывать колебания в контуре.
При их помощи можно описывать колебания в контуре.
Дата добавления: 2015-06-22; просмотров: 872;
