Определение показателей генеральной совокупности
При решении задачи на определение показателей генеральной совокупности предполагается, что генеральная совокупность соответствует нормальному закону распределения, поэтому может быть полностью отражена показателями средней арифметической (хген) и среднего квадратического отклонения (аген).
Средняя арифметическая генеральной совокупности определяется на основе показателей выборки и может быть отражена следующим образом:
*выб - mt < хген < хвыб + mt,
где хген — средняя арифметическая генеральной совокупности; *выб — средняя арифметическая выборки; т — ошибка репрезентативности (стандартная ошибка); t — критерий достоверности (критерий надежности). Показатель надежности /определяется по таблице приложения 4 по числу степеней свободы k, равному числу элементов выборки минус единица, т. е. k = п - 1. Для определения доверительных границ хген необходимо провести расчеты в соответствии с формулами (2.14).„(2.17).
Величины хвыб - mt и Зсвыб + mt называются нижней и верхней доверительными границами.
Величины т и t следует объяснить, исходя из основной идеи выборочного метода: если корректно составить выборку, то ее показатели правильно представляют генеральную совокупность. Так, в частности, из одной генеральной совокупности может быть избрано множество выборок. Установлено, что средние показатели этих выборок разнятся между собой практически на одну и ту же величину. Кроме того, средние показатели генеральной совокупности отличаются от выборочных на эту же величину т.
Ошибка репрезентативности (т) указывает на различие между генеральной и выборочной средней совокупностью. Критерий (t) — это показатель вероятности (надежности), согласно которому можно утверждать, что различие между средними показателями генеральной и выборочной совокупности не превышает величину ошибки т.
Отметим, что в практике спортивных исследований поступают таким образом: находят заранее определенную надежность, при которой исследователь удовлетворен точностью расчета. Обычно это надежность Р = 0,95.
Поскольку вероятность не может быть больше Р= 1,0, принято использовать не только понятие надежности Р, но и величину а = 1 - Р, показывающую уровень значимости. .
Таким образом, практика спортивных расчетов основана на надежности Р> 0,95 при уровне значимости а < 0,05. Это означает,
59 что спортивные расчеты, как правило, удовлетворяются точностью, при которой на каждые 100 испытаний 5 могут быть неточными.
Ошибка репрезентативности т находится по нижеприведенным формулам (2.14)...(2.17).
и = %£. (2.14)
Л/Л
Формула (2.14) применяется в случае, когда число элементов генеральной совокупности неизвестно (N= °°), а число элементов выборки л > 20:
°"выб
т =
(2.15)
Формула (2.15) применяется, когда число элементов генераль-ной совокупности неизвестно (N= °°), а число элементов выбор-ки и < 20:
т -

°выб
(2.16)
Формула (2.16) используется, если выборка велика, т.е. п > > 20, а число элементов N генеральной совокупности известно:
т =
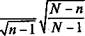
Овыб
(2.17)
Формула (2.17) используется, если выборка мала, т.е. л < < 20, а число элементов генеральной совокупности известно как N.
Для определения доверительных границ среднего квадратиче-ского отклонения генеральной совокупности (аген) используют метод сравнения
<W(1 - 9) * °ген JS о-выб(1 + Ф,
где авыб — среднее квадратическое отклонение выборки; q — величина, определяемая по таблице приложения 5.
При q < 0 сравнение преобразуется следующим образом:
0<оге„<авыб(1 + д).
Рассмотрим конкретный пример.
Пример 2.13. Группа спортсменов в количестве 30 человек (л) исследована на величину поглощения кислорода во время длительной работы Xj (л/мин). Испытуемые отобраны из 300 спортсменов N той же квалификации.
Оцените средние показатели 300 спортсменов. Исходные данные приведены в табл. 2.29.
Таблица 2.29 Обработка показателей поглощения кислорода 30 спортсменами
| № п/п | х. | и, | х,п, | Xj-X | (х,-х)2 | (х;-х)2л, |
| 4,0 | 20,0 | -0,3 | 0,09 | 0,45 | ||
| 4,2 | 25,2 | -0,1 | 0,01 | 0,06 | ||
| 4,3 | 34,4 | 0,0 | 0,00 | 0,00 | ||
| 4,5 | 18,0 | 0,2 | 0,04 | 0,16 | ||
| 4,6 | 18,4 | 0,3 | 0,09 | 0,36 | ||
| 4,7 | 14,1 | 0,4 | 0,16 | 0,48 | ||
| Всего | — | 130,1 | — | — | 1,51 |
« 4,33 = 4,3 л/мин; oLe = ~^ = 0,05 (л/мин)2; jv 30
<*выб = V°>05 - °. 22 л/мин.
Характеристика выборки из 30 спортсменов представляет хвыб± ± °выб = (4,3 ± 0,2) л/мин.
Для оценки генеральных показателей определим величину ошибки репрезентативности т. Поскольку в примере 2.13 объем генеральной совокупности N = 300, а выборка состоит из я = 30, т. е. л > 20, для определения ошибки репрезентативности используем формулу (2.17):
т =
Показатель t определяем по таблице приложения 4. При надежности Р = 0,95 (уровень значимости а = 0,05) и при числе степеней свободы Л = л - 1 = 30 - 1 = 29, / = 2,05.
Для оценки среднего квадратического отклонения определяем q по таблице приложения 5, где Р = 0,95 (а = 0,05); я = 30; q = 0,28.
Оценка генеральных показателей следующая:

-mt< хген <
mt;
4,3 - 0,03 • 2,05 < 5сген < 4,3 + 0,03 • 2,05;
4,3 - 0,06 < Зсген < 4,3 + 0,06;
4,24 < хген < 4,36;
0,2(1 - 0,28) <аген<; 0,2(1 +0,28);
61 0,2 • 0,72 <аген< 0,2 -1,28; 0,14<аген<0,26.
Таким образом, группа испытуемых из 30 спортсменов, характеризуемая как Зсвыб ± авыб = (4,3 ± 0,2) л/мин, позволяет оценить генеральную совокупность N из 300 спортсменов как
4,24 < хге„ < 4,36; 0,14<аген<0,26.
Доверительные границы можно определить в случае, если оценку средних показателей генеральной совокупности требуется выразить одним числом, т.е.
4,24 + 4,36
. . . = 4, 3 л/мин;
0,14 + 0,26 Л . ,
ен = - - - = 0, 2 Л/
,
МИН.
В этом случае показатели выборки и генеральной совокупности совпали, что свидетельствует о корректном подборе выборки.
В целом при характеристике генеральной совокупности обычно указывают на величины хген; т, т. е. хген = 4,3 л/мин, т = 0,03 л/мин.
Ошибка репрезентативности показывает, насколько хген может отличаться от Зсвыб при надежности Р = 0,95 (а = 0,05).
Другими словами, анализируя полученные данные, можно сделать вывод, что 30 испытуемых имеют среднюю величину поглощения кислорода во время длительной работы, равную 4,3 л/мин. Спортсмены в количестве 300 человек, из числа которых избраны 30 испытуемых, также покажут среднюю величину поглощения кислорода во время длительной работы, равную 4,3 л/мин. Однако утверждая это, мы ошибаемся на 0,03 л/мин с вероятностью 0,95.
Дата добавления: 2015-06-17; просмотров: 1799;
