Обработка показателей ЧСС до разминки
| № п/п | х, | "/ | х,п, | Xj-X | (х,-х)2 | (х,.-х)2л, |
| -7, | ||||||
| -3 | ||||||
| _1 | ||||||
| 6 . | ||||||
| Всего | — | — | — |
х = « 157,3 » 157 уд./мин; с2х = « 10,66 (уд./мин)2;
О 1о
сх = VlO,66 = 3,26 = 3,0 уд./мин.
Таким образом, до разминки показатели группы составили: х ± ± ах = (157 ± 3) уд./мин.
Таблица 2.31 Обработка показателей ЧСС после разминки
| № п/п | У' | "i | УМ | у! -У | (у, -у)2 | (У1-у)г«1 |
| 2 | -5 | |||||
| _з | ||||||
| Всего | — | — | — |
57 = 1Г = 169 уд-/мин;
= if = 8> 22
3,0 уд./мин.
Таким образом, после разминки показатели группы составили у - ву = (169 ± 3) уд./мин.
Теперь определим обе ошибки репрезентативности. Выявляется различие между средними показателями и некоей огромной генеральной совокупностью N = °°, которая нам фактически неизвестна и из которой избрана первая xh а затем вторая _у, выборки.
Для определения ошибки используем формулу (2.15), так как число членов генеральной совокупности неизвестно (N - °°) и объем выборки мал (менее 20 элементов). Таким образом,
= 0,73 уд./мин;
= 0,73 уд./мин.
Ошибки по обеим группам совпали, так как объемы выборок равны (исследуется одна и та же группа при различных условиях), а средние квадратические отклонения составили ах = ау = 3 уд./мин.
Переходим к определению критерия Стьюдента:
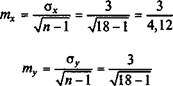
-У\ _ |157-169|
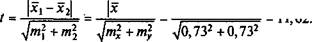
3 Начинская
65 Задаем надежность счета: Р = 0,95.
Число степеней свободы k = nt + л2 - 2 = 18 + 18-2 = 34. По таблице приложения 4 находим ^ф = 2,02.
Статистический вывод. Поскольку t = 11,62, а граничное /^ = = 2,02, то 11,62 > 2,02, т. е. t > t^, поэтому различие между выборками статистически достоверно.
Педагогический вывод. Установлено, что по показателю ЧСС различие между состоянием группы до и после разминки является статистически достоверным, т.е. значимым, принципиальным. Итак, по показателю ЧСС можно сделать вывод, что разминка эффективна.
Критерий Фишера является параметрическим. Он применяется при сравнении показателей рассеивания выборок. Это, как правило, означает сравнение по показателям стабильности спортивной работы или стабильности функциональных и технических показателей в практике физической культуры и спорта. Выборки могут быть разновеликими.
Критерий Фишера определяется в нижеприведенной последовательности.
1. Находим Критерий Фишера Fno формуле
F
г =
(2.19)
где о2, а2. — дисперсии сравниваемых выборок.
Условиями критерия Фишера предусмотрено, что в числителе формулы (2.19) находится большая дисперсия, т.е. число Fвсегда больше единицы.
2. Задаем надежность счета: Р = 0,95 — и определяем числа степеней свободы для обеих выборок: ki = п{ - 1; k2 = я2 - 1.
3. По таблице приложения 4 находим граничное значение критерия f^.
4. Сравнение критериев Fw F^ позволяет сформулировать выводы:
- если F > /Vp, то различие между выборками статистически достоверно;
- если F< /Vp, то различие между выборками статически недостоверно.
Приведем конкретный пример.
Пример 2.15. Проанализируем две группы гандболистов: х/ (п{ = = 16 человек) и yf (и2 = 18 человек). Эти группы спортсменов исследованы на время отталкивания (с) при броске мяча в ворота.
Однотипны ли показатели отталкивания?
Исходные данные и основные расчеты представлены в табл. 2.32 и 2.33.
Таблица 2.32 Обработка показателей отталкивания первой группы гандболистов
| № п/п | X, | «/ | х,п, | Xj X | to-*)2 | (х,-х)2п, |
| 0,18 | 0,54 | 0,02 | 0,0004 | 0,0012 | ||
| 0,17 | 0,51 | 0,01 | 0,0001 | 0,0003 | ||
| 0,16 | 0,64 | 0,00 | 0,0000 | 0,0000 | ||
| 0,15 | 0,45 | -0,01 | 0,0001 | 0,0003 | ||
| 0,14 | 0,28 | -0,02 | 0,0004 | 0,0008 | ||
| 0,13 | 0,13 | -0,03 | 0,0009 | 0,0009 | ||
| Всего | — | 2,55 | — | — | 0,0035 |
-0,0002 с'.
Таблица 2.33 Обработка показателей отталкивания второй группы гандболистов
| № п/п | у! | «, | УМ | у! -У | (У, -У)2 | (и -у)2 и/ |
| 0,18 | 0,54 | 0,05 | 0,0025 | 0,0075 | ||
| 0,14 | 0,70 | 0,01 | 0,0001 | 0,0005 | ||
| 0,13 | 0,78 | 0,00 | 0,0000 | 0,0000 | ||
| 0,12 | 0,24 | -0,01 | 0,0001 | 0,0002 | ||
| 0,11 | 0,11 | -0,02 | 0,0004 | 0,0004 | ||
| 0,10 | 0,10 | -0,03 | 0,0009 | 0,0009 | ||
| Всего | — | 2,47 | — | — | 0,0095 |
у = =l^. = о, 14 с; а2 = ^^ = 0,0005 с2.
"У18
Й
Определим критерий Фишера:
р - £? - & - М°_Р5
„2
= 2,5.
* а2 а2 0,0002
Числитель критерия а2 = 0,0005 с2 > а,2 = 0,0002 с2. Зададим надежность Р = 0,95 (а = 0,05) и определим числа степеней свободы для каждой группы:
kx = л, - 1 = 16 - 1 = 15;
67 ky = n2 - 1 = 18 - 1 = 17.
По данным, представленным в таблице приложения 6, находим /k /^ = 2,4.
Обратим внимание на то, что в таблице приложения 6 перечисление чисел степеней свободы как большей, так и меньшей дисперсии при приближении к большим числам становится грубее Так числа степеней свободы большей дисперсии следует в таком порядке: 8, 9, 10, 11, 12, 14, 16, 20, 24 и т.д., а меньшей -28, 29, 30, 40, 50 и т.д.
Это объясняется тем, что при увеличении объема выборок различия /"-критерия уменьшаются и можно использовать табличные значения, приближенные к исходным данным. Так, в примере 2.15 k = 17 отсутствует и можно принять ближайшее к нему значение k = 16, откуда и получаем /^ = 2,4.
Статистический вывод. Поскольку критерий Фишера F= 2,5 > > F = 2,4, выборки различимы статистически достоверно.
Педагогический вывод. Значения времени отталкивания (с) при броске мяча в ворота у гандболистов обеих групп существенно различаются. Эти группы следует рассматривать как различные.
Дальнейшие исследования должны показать, в чем причина
такого различия.
Критерий Вилкоксона является непараметрическим. Он применяется для выборок одинакового объема при попарном сравнении их элементов.
Критерий Вилкоксона определяется так.
1. Задаем надежность счета и определяем число степеней свободы как k = п - 1, где п — количество пар элементов обеих групп. По таблице приложения 7 находим граничное значение W^.
2. Сравнение критериев Wn W^ позволяет сделать выводы:
- если W> И^р, различие между выборками статистически недостоверно;
- если W < И^р, различие между выборками статистически
достоверно.
Для нахождения критерия Вилкоксона W используют порядковый номер (ранг) разности каждой пары элементов выборок.
Приведем конкретный пример.
Пример 2.16. Группа конькобежцев показала время (с) в беге на 30 м: х, — в начале и у, — в конце серии тренировок. Эффективна ли серия тренировок?
Исходные данные примера и основные расчеты представлены в табл. 2.34.
Для нахождения Ж по таблице приложения 7 произведем следующие действия.
1. Определим разность каждой пары исходных значений с точным указанием ее знака, т. е. х/ - у/.
Таблица 2.34 Определение эффективности тренировки конькобежцев
| № п/п | *,• | у! | х, - У, | W | Щ+) | Щ-) |
| 4,15 | 4Д2 | 0,03 | 3,5 | 3,5 | — | |
| 4,17 | 4,20 | -0,03 | 3,5 | — | 3,5 | |
| 4,20 | 4,15 | 0,05 | 6,0 | 6,0 | — | |
| 4,22 | 4,25 | -0,03 | 3,5 | — | 3,5 | |
| 4,24 | 4,26 | -0,02 | 1,0 | — | 1,0 | |
| 4,25 | 4,22 | 0,03 | 3,5 | 3,5 | — | |
| Всего | — | _ | — | — | 13,0 | 8,0 |
2. Всем разностям присвоим ранги, т. е. назначим номера в порядке их возрастания. При этом знак разности не учитывается.
В данном примере наименьшее значение имеет разность 0,02, так как ее ранг равен единице. Затем по абсолютному значению найдем ранг 0,03. Значений, соответствующих xh четыре (4,15; 4,17; 4,22 и 4,25) и они получают одинаковый ранг, поровну разделив между собой места по порядку 2, 3, 4 и 5, которые были бы им присвоены, если бы они были разными. Поскольку они одинаковы, их ранг равен (2 + 3 + 4 + 5)/4 = 3,5.
Таким образом, первые четыре ранга уже определены.
Величина 0,05 по абсолютному значению следует после 2, 3, 4 и 5, поэтому она должна иметь ранг, равный 6. Таким образом, в графе W (см. табл. 2.34) находятся ранги всех разностей без учета их знака.
Теперь учтем знаки. С этой целью выпишем ранги положительных разностей в графе W(+), а отрицательных — в графе W(-). Выписанные ранги просуммируем — меньшая из этих сумм является критерием Вилкоксона. В данном случае W= 8,0.
Теперь зададим надежность счета: Р- 0,95 (а = 0,05) при количестве сравниваемых пар, равном 6, — и по таблице приложения 7 найдем граничное значение W^ = 1.
Статистический вывод. Сравниваемые выборки различимы статистически недостоверно, так как W - 8,0 > W^ - 1,0.
Педагогический вывод. Сравниваемые выборки несущественно различны, и потому можно заключить, что группа испытуемых провела неэффективную серию тренировок.
Критерий Уайта является непараметрическим. При помощи этого критерия сравнивают две различные по объему, но небольшие выборки. Группы, содержащие большое количество пар, приводят к громоздким вычислениям.
Критерий Уайта определяется следующим образом,
69 1. Задаем надежность счета при двух объемах выборки «[ и п2.
2. По таблице Уайта (см. приложение 8) находим величину граничного критерия Уайта 7^.
3. Сравнение критериев Ти Т^ позволяет сделать выводы:
- если Т > Гц,, то различие между сравниваемыми группами статистически недостоверно;
- если Т < Ггр, то различие статистически достоверно. Решим пример, используя критерий Уайта.
Пример 2.17. Две группы спортсменов (х,) и (у,) исследованы на гибкость. У спортсменов измерена амплитуда наклона (см). Сравните гибкость спортсменов первой и второй групп.
Исходные данные приведены в табл. 2.35 и 2.36.
Таблица 2.35
Дата добавления: 2015-06-17; просмотров: 2919;
