IV. Обработка результатов измерений. 1. Для каждого режима определить коэффициент вязкости по формуле (3.5).
1. Для каждого режима определить коэффициент вязкости по формуле (3.5).
2. Найти среднее значение коэффициента вязкости и определить абсолютную и относительную погрешность его измерения (см. введение).
3. Для каждого режима посчитать число Рейнольдса по формуле (3.7) и занести в таблицу.
V.Выводы:1)Коэффициент динамической вязкости воздуха при комнатной температуре η=(…±…) Па·с.
2) Число Рейнольдса лежит в интервале от… до…, следовательно течение воздуха в капилляре ламинарное.
Контрольные вопросы
1. Охарактеризуйте явления переноса в газах, напишите основные уравнения переноса.
2. В чём заключается физический смысл коэффициентов вязкости, теплопроводности, диффузии?
3. В чём заключается капиллярный метод определения коэффициента вязкости?
4. Связь каких параметров определяется формулой Пуазейля? Каковы условия её применения?
5. Как изменяется скорость движения газа по радиусу канала при ламинарном режиме течения?
6. Каким образом, проводя измерения расхода воздуха, разности давлений на концах капилляра, можно определить значения величины 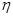 ?
?
7. Ламинарное и турбулентное течение жидкости. Критерий Рейнольдса.
8. Какие жидкости называют ньютоновскими?
Литература
1. Белановский А.С. Основы биофизики в ветеринарии/ М.: Агропромиздат, 1989. – 272 с.
2. Ремизов А.Н. Медицинская и биологическая физика/ М.:Высшая школа, 1987. – 638 с.
3. Трофимова Т.И. Курс физики: Учеб. пособие. М: Высшая школа, 1985. 432 с.
4. Детлаф А.А., Яворский Б.М. Курс физики: Учеб. пособие. М: Высшая школа, 1989. 608 с.
Вопросы для защиты в форме круглого стола
По I разделу
«Термодинамика. Молекулярно-кинетические явления переноса»
| № Пп | Вопросы | Рекоменд. Литература | |
| №. | Стр. | ||
| Какие системы называют термодинамическими? Параметры состояния термодинамической системы. | 216-217 72-73 88-90 | ||
| Идеальный газ. Уравнение состояния идеального газа. | 73-76 | ||
| Изопроцессы: изотермический, изобарный, изохорный, адиабатный. Уравнения их состояний. | 93-94 | ||
| Адиабатный процесс; уравнение Пуассона. | 94-95 | ||
| Внутренняя энергия идеального газа. Работа расширения идеального газа. Первое начало термодинамики. | 88-90 218-219 | ||
| Виды теплообмена. Теплообмен в живых организмах. | 94-96 | ||
| Теплоемкость вещества – удельная и молярная. Теплоемкость Ср и Сv. Уравнение Майера. | 91-92 | ||
| 1 начало термодинамики в живых организмах. Открытие Майера. | 94-95 | ||
| Экзотермические реакции в живых организмах. | 97-98 | ||
| Пути получения тепла организмом. Удельная теплота сгорания жиров, белков, углеводов. Закон Гесса. | 95-96 | ||
| Способы отвода тепла. Механизмы терморегуляции организма. | 105-109 | ||
| Теплопродукция. Диаграмма трансформации энергии в системе организм – внешняя среда. | 98-104 | ||
| Масса животного и энергетический обмен. | 68-71 | ||
| Циклы, приведенная теплота. Термодинамическое и вероятностное толкование энтропии. | 97-98 | ||
| Энтропия. II начало термодинамики. Почему невозможна «тепловая смерть» Вселенной? | 228-230 | ||
| Понятие о термодинамике открытых систем; теорема Пригожина. | 116-120 233-235 | ||
| II начало термодинамики для живых систем. | 112, 118-119 | ||
| Принцип Ле Шателье – Брауна. Примеры его реализации при взаимодействиях физических и биологических объектов. | 120-121 | ||
| Термодинамические методы лечения в ветеринарии. | 110-112 | ||
| Явления переноса в неравновесных системах: диффузия (закон Фика), теплопроводность (закон Фурье). | 83-85 | ||
| Явление вязкого трения в жидкостях и газах. Закон Ньютона. | |||
| Сущность метода Стокса для определения вязкости. | 18-19 | ||
| Сущность метода Пуазейля для определения вязкости. | 16,114 | ||
| Течение идеальной жидкости. Уравнение неразрывности струи. Закон Бернулли. | 51-54 | ||
| Ламинарное и турбулентное течение. Число Рейнольдса. | 15-18 | ||
| Характер течения крови в артериях, венах, капиллярах; его зависимость от вязкости крови и состояния сосудов. | 27-33 | ||
| Суть метода Короткова для измерения кровяного давления. | 34-37 |
Рекомендуемая таблица вариантов вопросов для проведения круглого стола
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | В9 | В10 | |
РАЗДЕЛ II. КОЛЕБАНИЯ. ВОЛНЫ.
ВВЕДЕНИЕ
Общие положения
I. Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Например, чередование фаз активности и пассивности в поведении человека и животных, повторяющиеся регулярные процессы при обмене веществ, пульсирующая работа сердца и др. Это сложные колебательные процессы, но они могут быть сведены к сумме простых колебаний с помощью Фурье-анализа [4, с.227].
Простейшими и наиболее распространенными в природе и технике являются гармонические колебания.
Уравнение механических гармонических колебаний имеет вид
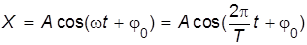 (II.1)
(II.1)
где Х – смещение сосредоточенной массы (материальной точки) от положения равновесия (м);
А – амплитуда колебаний (м);
Т – период колебаний (сек);
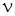 – частота колебаний (1/сек);
– частота колебаний (1/сек);
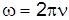 – циклическая частота (1/сек);
– циклическая частота (1/сек);
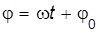 – фаза колебаний (рад);
– фаза колебаний (рад);
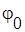 – начальная фаза (рад).
– начальная фаза (рад).
Так как уравнение (II.1) по существу дает зависимость пути (смещения) колеблющейся точки от времени 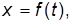 то выражение для скорости будет иметь вид
то выражение для скорости будет иметь вид
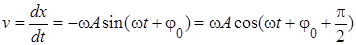 (II.2)
(II.2)
а для ускорения
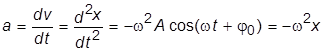 (II.3)
(II.3)
Таким образом, при гармоническом колебательном движении скорость и ускорение также, как и смещение, изменяются гармонически. При этом скорость опережает смещение на 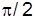 , а ускорение прямо пропорционально смещению и находятся с ним в противофазе.
, а ускорение прямо пропорционально смещению и находятся с ним в противофазе.
Колебания, совершающиеся под действием сил, определяемых устройством самой колебательной системы, называют собственными колебаниями. Собственные гармонические колебания совершаются под действием упругих или квазиупругих сил. Частота собственных колебаний, обусловленных действием возвращающей силы с коэффициентом упругости k равна:
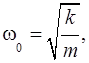 (II.4)
(II.4)
а период
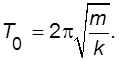 (II.5)
(II.5)
Как правило, на практике колебания совершаются в вязкой среде (газ, жидкость). В связи с этим колебания будут затухать, и амплитуда колебаний будет убывать во времени.
Если ввести величину 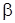 , называемую коэффициентом затухания, то при
, называемую коэффициентом затухания, то при 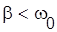 свободные затухающие колебания описываются зависимостью:
свободные затухающие колебания описываются зависимостью:
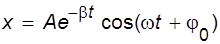 (II.6)
(II.6)
что графически представлено на рис. II.1.
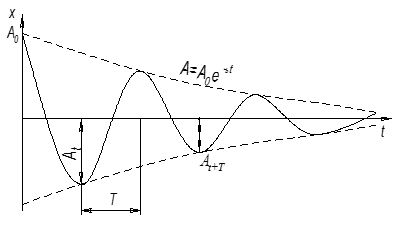
Рис.II.1. Графическое изображение свободного затухающего колебания
Из формулы (II.6) и графика видно, что амплитуда убывает по закону экспоненты:
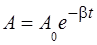 . (II.7)
. (II.7)
Частота и период затухающих колебаний с увеличением коэффициента затухания становятся более медленными и соответственно равны:
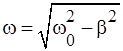 ; (II.8)
; (II.8)
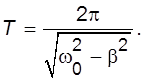 (II.9)
(II.9)
Из этих выражений следует, что при 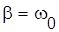 период колебаний становится равным бесконечности, и затухающий периодический процесс переходит в апериодический.
период колебаний становится равным бесконечности, и затухающий периодический процесс переходит в апериодический.
Декрементом затухания называют отношение значения амплитуд, соответствующих моментам времени, отличающимся на период (см. рис.II.1),
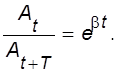 (II.10)
(II.10)
Логарифм этого отношения называют логарифмическим декрементом затухания
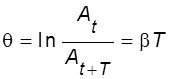 (II.11)
(II.11)
Время, в течение которого амплитуда колебаний уменьшается в е раз, называют временем релаксации t.
В таком случае
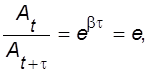
и, следовательно,
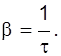 (II.12)
(II.12)
Логарифмический декремент затухания можно определить, зная период и коэффициент затухания, при этом он равен обратной величине числа полных колебаний 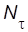 , совершенных за время релаксации
, совершенных за время релаксации
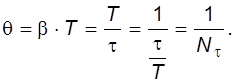 (II.13)
(II.13)
II. Волной называют процесс распространения колебаний в пространстве. Поэтому смещение колеблющейся точки волны является функцией не только времени, но и координат. В основе изучения волновых процессов лежит бегущая гармоническая волна. В случае распространения волны вдоль оси Х уравнение такой волны имеет вид:
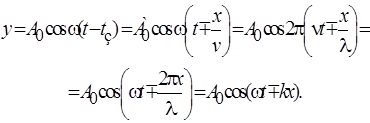 (II.14)
(II.14)
Здесь 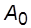 – амплитуда;
– амплитуда;
ω – круговая (циклическая) частота волны;
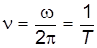 – частота волны;
– частота волны;
T – период колебаний волны;
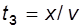 – время запаздывания;
– время запаздывания;
х – расстояние от источника колебаний от точки наблюдения;
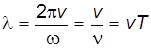 – длина волны;
– длина волны;
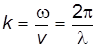 – волновое число.
– волновое число.
Знак (–) соответствует волне, бегущей в положительном направлении оси Oх.
Если направление распространения волны совпадает с направлением колебаний частиц среды, то волна – продольная. Если частицы колеблются в плоскости, перпендикулярной направлению распространения волны, то волна называется поперечной. В твердых телах могут распространяться как те, так и другие волны, а в жидкостях и газах – только продольные.
Колебания, частоты которых лежат в интервале от 20 до 20000 Гц, обладают свойством вызывать ощущение звука и могут быть выделены по этому признаку в особую группу звуковых или акустических колебаний, называемых звуком.
Упругие волны, частота которых выше 20000 Гц называются ультразвуком. Ультразвук (УЗ) нашел широкое применение в медицине и ветеринарии. Например, ультразвуковой диагностический эхо-метод, основанный на различном отражении УЗ от участков с различной плотностью тканей. Динамические процессы в органах наблюдают с помощью УЗ метода с использованием эффекта Доплера, когда частота колебания изменяется при движении источника звука или наблюдателя. Поскольку звуковая волна переносит энергию, УЗ применяют также как физиотерапевтическое средство и даже как хирургический инструмент.
Упругие волны, частота которых ниже 20 Гц называются инфразвуком. Инфразвук (ИЗ) вызывает вынужденные колебания внутренних органов, что приводит к нарушению их работы. Это особенно опасно при возникновении резонансных явлений, поскольку частоты собственных колебаний крупных внутренних органов лежат в диапазоне от 2 до 17 Гц.
Как показано в теории волн (в случае постоянства модуля упругости и плотности среды), волна (II.14) удовлетворяет волновому дифференциальному уравнению
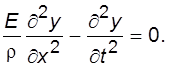 (II.15)
(II.15)
Дважды дифференцируя (II.14) (один раз – по х, другой – по t), можно убедиться в следующем:
1) (II.14) является решением (II.15) при любых амплитудах и частотах ω;
2) между скоростью v распространения волнового процесса, модулем упругости Е и плотностью среды r существует связь
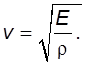 (II.16)
(II.16)
Из (II.16) следует, что скорость продольных волн зависит от модуля упругости (Юнга) Е (поперечных – от модуля сдвига .). Можно убедиться, что решением уравнения (II.15) является также следующее выражение, представляющее собой сумму:
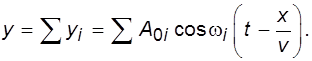 (II.17)
(II.17)
Уравнение (II.17) является математически выражением основного свойства волновых процессов – принципа суперпозиции (наложения) волн. При суперпозиции волны разных частот просто накладываются одна на другую, не возмущая друг друга, следовательно, интенсивности их в любой точке пространства складываются. При сложении волн одинаковой частоты наблюдается интерференция.
ЛАБОРАТОРНАЯ РАБОТА № 4 (1-10)
Дата добавления: 2015-06-22; просмотров: 2977;
