Обработка показаний становой силы спортсменов
| № п/п | хi | пi | хi пi | хi - X | (хi – X)² | (хi - X)² пi | t = хi- X σ | f(t) | kn/σ | f(k) округленно |
| 9,4 | 9,4 | -0,8 | 0,64 | 0,64 | -2,00 | 0,0540 | 1,539 | |||
| 9,6 | 48,0 | -0,6 | 0,36 | 1,80 | -1,50 | 0,1295 | 3,690 | |||
| 9,8 | 58,8 | -0,4 | 0,16 | 0,96 | -1,00 | 0,2420 | 6,897 | |||
| 9,9 | 109,9 | -0,3 | 0,09 | 0,99 | -0,75 | 0,3011 | 8,581 | |||
| 10,2 | 122,4 | 0,0 | 0,00 | 0,00 | 0,00 | 0,3989 | 11,343 | |||
| 10,3 | 103,0 | 0,1 | 0,01 | 0,10 | 0,25 | 0,3867 | 11,020 | |||
| 10,5 | 73,5 | 0,3 | 0,09 | 0,63 | 0,75 | 0,3011 | 8,581 | |||
| 11,0 | 33,0 | 0,8 | 0,64 | 1,92 | 2,00 | 0,0540 | 1,539 | |||
| 11,2 | 22,4 | 1,0 | 1,00 | 2,00 | 2,50 | 0,0488 | 1,391 | |||
| Все-го | — | 579,4 | — | — | 9,04 | — | — | — |
o-2=°6=0,4H; — =
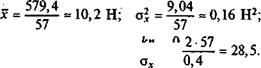
В табл. 2.28 показана величина х2 = 3,95. По таблице приложения 2 находим
Тогда
= 3,95 = 4,0 и k=6. ^ х2) = 0,6767.
55 Таблица 2.28
Расхождение между теоретическими и практическими частотами.
Вариант 2
| № п/п | X, | «/ | и,° | ni - «,° | (ni-nf? | (nt-npf/n? |
| 9,4 | -1 | 0,50 | ||||
| 9,6 | 0,25 | |||||
| 9,8 | _^ | 0,14 | ||||
| 9,9 | 0,44 | |||||
| 10,2 | 0,09 | |||||
| 10,3 | -1 | 0,09 | ||||
| 10,5 | -2 | 0,44 | ||||
| 11,3 | 1,00 | |||||
| 11,2 | 1,00 | |||||
| Всего | — | — | — | 3,95 |
Полученная вероятность значительно больше вероятности 0,01. Следовательно, исходный эмпирический ряд соответствует нормальному закону.
Данные, приведенные в табл. 2.25 — 2.28, показывают, что распределение частот, полученное на практике, может быть близко или далеко от нормального закона. Отсюда, чтобы иметь право пользоваться свойствами нормального закона, нужно всегда проверять их на соответствие.
Правило трех сигм (±30) (см, рис. 2.9) является еще одним способом проверки эмпирического ряда на соответствие нормальному закону распределения. Этот способ — приближенный. Суть его сводится к следующему.
Установлено, что под кривой Гаусса участок х ± о занимает 0,6828 всей площади, участку Зс ± 2d отведено 0,9545 всей площади, а на участке х ± За находится 0,9973 всей площади. Обратим внимание на то, что вероятность, откладываемая по оси ординат, прямо пропорциональна числу рассматриваемых событий, т. е. числу благоприятствующих событий, поэтому можно с уверенностью заключить, что на участке Зс ± За сосредоточено 0,9973 всех частей. В этом случае исследуемый закон является нормальным.
Рассмотрим пример 2.12 (см. табл. 2.27, графы 1, 2). Если объем совокупности (сумма частот) п = 57, то 0,9973 объема составляет 56,8461» 57. Таким образом, если на участке 5с ± За сосредоточится весь объем совокупности, закон можно рассматривать как нормальный.
Проанализируем данные, приведенные в табл. 2.27:
л = 10,2; а = 0,4; За = 0,4- 3 = 1,2; х - За = 10,2 - 1,2 = 9,0; х + За = 10,2 + 1,2 = 11,4,
т.е. если на участке 9,9... 11,4 сосредоточены все 57 испытуемых, то распределение соответствует нормальному закону.
Впримере 2.12 так и получилось. По вертикали наш размах составил от 9,4 до 11,2, т.е. на участке 9,4... 11,2 сосредоточено 57 испытуемых. Размах 9,4... 11,2 меньше, чем 9,9... 11,4; Объясним это так: варианты 9,4; 9,5; 9,6; 9,7; 9,8 равны 0, варианты 11,3; 11,4 также равны 0.
Итак, эмпирическое распределение, данные которого представлены в табл. 2.28 (графы 1, 2), согласно правилу трех сигм (±3<т) соответствует нормальному закону распределения.
Нормальный закон распределения имеет место тогда, когда на появление случайных событий одновременно оказывают влияние множество факторов, причем невозможно установить приоритет какого-либо из факторов.
В ФКС, как правило, рассматриваются именно такие ситуации. Объясняется это тем, что спорт зависит от человеческого фактора, который определяется множеством факторов, и все они одинаково необходимы, важны и влиятельны. В силу этого нормальному закону соответствуют антропометрические показатели (рост, масса тела и т.д.), физиологические факторы (МПК, ЖЕЛ, ПАНО и др.), психологические, педагогические, а также собственно спортивные показатели, например спортивные результаты. Итак, нормальный закон и задачи, решаемые на основе свойств нормального закона, имеют огромное значение в практике спортивных исследований.
Дата добавления: 2015-06-17; просмотров: 1343;
