Обработка результатов измерений амплитуды наклонов
| № п/п | хi | ni | xini | xi-X | (xi-X) | (xi-X)n² |
| -12 | ||||||
| -6 | ||||||
| -2 | ||||||
| Всего | — | — | — |
X = 1266 = 42,2 ≈ 42 мм; σx² = 514 = 17,133 мм;
30 30
σx = √17,133 = 4,14 ≈ 4мм;
X ± σx =(42 ± 4) мм.
На основании данных, приведенных в табл. 2.24, построим полигон (рис. 2.5). Полигон выражает соотношение между показателями амплитуды наклона хiи частотой их появления ni. Такое соотношение называется практическим распределением. Оно получено в результате экспериментальных наблюдений.
Начнем преобразование полигона (см. рис. 2.5). Прежде всего отметим, что частота появления события ni может рассматриваться как число, благоприятствующее появлению события хi, а равновозможным можно представить объем совокупности, в данном случае ni= 30. Таким образом, шкала ординат может быть выражена вероятностями появления хiт.е.
Р(хi) = ni/n.(2.8)
От такого представления полигон не изменится, другим будет только масштаб шкалы ni.

Рис. 2.5. Полигон (см. табл. 2.24)
Затем представим, что спортсменов, исследуемых на гибкость, было очень много и каждое из представленных на шкале хi имело бы свою частоту. В этом случае точки на графике очень тесно прилегали бы друг к другу, образуя сплошную плавную кривую. Эта кривая в принципе отразила бы факт соотношения величин х, и и, для случая, когда все возможные х, приняты во внимание. Такое распределение называется теоретическим распределением. Оно представляет собой закономерность соотношения между показателями хi иni.
Математическая статистика предоставляет в распоряжение исследователя теоретические распределения, выраженные языком математики, свойства которой могут быть использованы на практике.
Для практических исследований такие распределения нужны при решении двух задач.
Во-первых, установив, что эмпирическое распределение соответствует определенному теоретическому, представляется возможным использовать известные и апробированные свойства теории на практике. В этом случае проблема заключается в том, чтобы установить и доказать схожесть эмпирического и теоретического распределений. Во-вторых, с помощью точного теоретического распределения возможно установить вероятностное положение конкретной единицы совокупности по отношению ко всем прочим единицам. В силу этих двух задач теоретические распределения имеют существенное значение для практических исследований.
Известно около двадцати теоретических распределений. Одни из них отражают соотношение редких и малоизученных явлений, другие — равномерность возникновения единиц совокупности и т. д.
Самым распространенным, хорошо изученным и практически полезным распределением принято считать нормальное распределение, отражаемое кривой Гауссаи известное как нормальный закон.
Смысл этого распределения заключается в том, что оно отражает массовые однотипные явления — именно такие, которые рассматривает статистика. Основой этого распределения является закон больших чисел, доказанный теоремой А. А. Ляпунова.
Закон больших чисел рассматривает ситуацию, при которой утверждается, что с любой вероятностью близкой к 1, отклонение средней арифметической достаточно большого числа случайных величин от некоторой постоянной величины не превзойдет заданного, как угодно малого положительного числа.
Другими словами, рассматриваются случайные величины, на которые воздействует множество Независимых факторов. Факторы влияют на величину по-разному, но если их достаточно много, то отдельные влияния взаимно погашаются и средняя случайных величин практически не отклоняется от постоянного значения.
Смысл теоремы А. А. Ляпунова заключается в том, что на случайные величины одновременно влияет множество независимых факторов, действие которых в отдельности значительно меньше их суммарного действия, они распределяются в соответствии с нормальным законом. Таким образом, если на какую-то случайную величину действует множество факторов, не имеющих очевидных преимуществ друг перед другом по степени влияния на эту величину, следует ожидать нормального закона распределения.
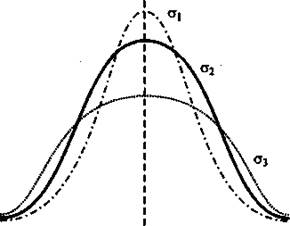
Теперь рассмотрим само распределение. Идея нормального распределения в том, что множество единиц совокупности распределяется таким образом, чтобы около средней арифметической было сконцентрировано наибольшее количество единиц, около больших или малых значений — минимальное количество единиц, а все прочие единицы должны соответствовать кривой Гаусса (рис. 2.6).

=
I
Рис. 2.6. Кривая Гаусса
Нормальный закон распределения представляет собой частный случай распределения, когда X = 0, а σ = 1. В данном случае X = 0 и ось ординат проходит через X.
Рассмотрим свойства нормального закона распределения.
1. От величины X зависит положение кривой: с увеличением (уменьшением) X кривая будет сдвигаться вправо (влево) вдоль оси абсцисс, при этом ее форма соответственно не изменяется.
2. От величины среднего квадратического отклонения σ зависит форма кривой: чем среднее квадратическое отклонение σ больше, тем ниже и шире кривая; чем среднее квадратическое отклонение σ меньше, тем выше и тоньше кривая (рис. 2.7).
 Р(хi)
Р(хi)
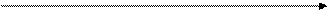
X xi σ < σ < σ
Рис. 2.7. Кривая Гаусса при разных величинах дисперсии σ
3. Формула нормальной кривой имеет вид
-(xi-X)²
Р(хi) = 1 · е 2 σ²
σ√2π , (2.9)
где Р (xi) — ординаты кривой; Xi— абсциссы кривой; X — средняя арифметическая величина; σ — среднее квадратическое отклонение; е — основание натуральных логарифмов.
Параметры X = 0 и σ = 1 показывают нормированную кривую, поэтому ее формула имеет вид
-xi²
Р(хi) = 1 · е 2
√2π , (2.10)
При построении кривой по эмпирическим данным формула выглядит так:
-t²
Р(хi) = kn · 1 · е 2
σ √2π , (2.10)
где k — величина интервала в вариационном ряду; n — объем совокупности; t — нормированное отклонение.
Нормированное отклонение находим по формуле:
t = xi – X . (2.12)
σ
51 Величина f(t) табулирована и может быть определена по таблице приложения 1.
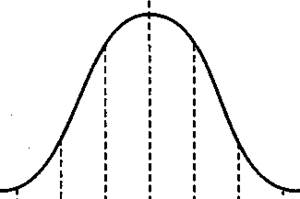
В некоторых задачах нормальное распределение представляется в виде так называемых z-оценок. В этом случае на оси ординат откладываются величины нормированных отклонений (рис. 2.8).
 Р(хi)
Р(хi)

0 -3,0 -2,0 -1,0 0 1,0 2,0 3,0 t
Рис. 2.8. Нормальное распределение (z-оценки)
Дата добавления: 2015-06-17; просмотров: 990;
