Физическое уравнение

Изучим связь между деформациями и внутренними усилиями элементов расчетной модели стержневой системы.

Выбранная нами расчетная модель сооружения такова, что механические и геометрические характеристики ее отдельных элементов постоянны, а внешняя нагрузка действует только в узлах. В этом случае по нескольким конечным значениям усилий в элементах расчетной модели можно определять усилия во всех точках стержней.

В расчетных моделях плоской стержневой системы встречаются три типовых элемента: 1) элемент с двумя жесткими узлами, 2) элемент с шарнирным и жестким узлами, 3) элемент с двумя шарнирными узлами. При их рассмотрении введем следующие обозначения: e^r – некоторый элемент, r – номер этого элемента.

1) Элемент с двумя жесткими узлами (рис. 13.2 а). В нем продольная и поперечная силы постоянны, а Q можно выразить через начальный и конечный моменты элемента: .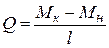

2) Элемент с шарнирным и жестким узлами (рис. 13.2 б), в котором поперечную силу можно выразить через конечный момент: .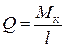

3) Элемент с двумя шарнирными узлами (рис. 13.2 в. В нем имеется лишь постоянная продольная сила N.

а) б)

в)

Рис. 13.2

Зависимость между внутренними усилиями и деформациями этих элементов может быть установлена через обобщенный закон Гука и записана в матричной форме

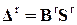, (2)

где 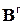– матрица податливости элемента, связывающая вектор перемещений элемента 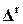с вектором усилий .

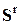Например, в элементе 1-го типа связь между компонентами векторов перемещений 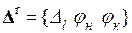и внутренних усилий 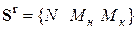выражается формулами (даются без вывода)

,

,

.

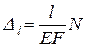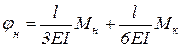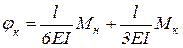Если эти уравнения записать в матричной форме (2), то матрица податливости элемента первого типа будет

.

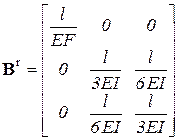Для элемента второго типа имеем

, , .

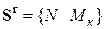Для элемента третьего типа

, , .

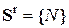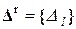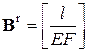Теперь рассмотрим полную дискретную модель сооружения как состоящую из m элементов 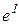, ,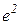…, 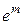. Для всех этих элементов можно записать уравнения (2), связывающие вектора деформаций элементов 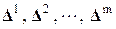с векторами усилий 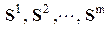. Если же объединить эти уравнения в общую систему, а вектора деформаций и усилий отдельных элементов объединить в вектора 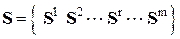и 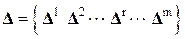, то полученную систему уравнений можно записать в виде одного матричного уравнения

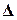=BS.

Оно, как устанавливающее связь между разными физическими величинами расчетной модели, называется физическим уравнением, где матрица

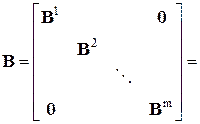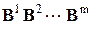é û

называется матрицей податливости системы. Здесь знак é û означает диагональность матрицы.