Графический метод сложения колебаний

Применим теперь для определения амплитуды световых колебаний в точке Р графический метод сложения колебаний, описанный в разделе 13.2. Для этого мысленно разделим волновую поверхность σ, затягиваю­щую отверстие в экране, на узкие кольца. При помощи формулы (13.7) запишем следующее выражение для колебания dEi, возбуждаемого в точ­ке Р вторичной световой волной, пришедшей в эту точку от кольца под номером i:

dE_i = dE_m, cos(wt-kR_i + a_A), (13.15)

где i= 0, 1, 2, ..., N; N - число колец,

dE_m=K(θ)( 2πr E_A/(a+b)) dR_i (13.16)

- амплитуда колебания; R_i - расстояние от внутреннего края i-го кольца до точки Р.

Пусть расстояния R_i от краев колец до точки Р таковы, что их раз­ность для любых двух соседних колец принимает одно и то же значение, т.е. не зависит от номера кольца:

R_i - R_i-1 = dR = const

Отсюда следует, что

R_i = R₀ +idR

(13.18)

Из рис. 13.4 видно, что при увеличении радиуса кольца угол θ уве­личивается. При этом коэффициент К(θ) уменьшается. Поэтому, как следует из формул (13.16) и (13.17), амплитуда dE_mi колебания в точке Р, вызванного вторичной световой волной, пришедшей от узкого кольца, также уменьшается при увеличении его радиуса. Иначе говоря, ампли­туда dE_mi колебания, возбуждаемого вторичной волной от г-го кольца, уменьшается при увеличении его номера i.

Представим каждое гармоническое колебание dE_i вектором dA_i,. Дли­на этого вектора равна амплитуде dE_mi колебания, а угол между ним и осью абсцисс - разности фаз ∆φ_i,_о колебаний dE_i и dE₀, возбуждае­мых волнами от i-го кольца и маленького сегмента в центре О волновой поверхности σ. Из формул (13.15) и (13.18) следует, что

∆φ_i,_о = k(R_i-R₀)= k i dR (13.19)

Амплитуда А суммарного колебания

E =∑_i=1^N dE_i (13.20)

равна длине вектора А суммы векторов

A =∑_i=1^N dA_i (13.21)

Для того чтобы найти сумму векторов dA_i, следует расположить эти векторы следующим образом. Вектор dA₀ можно расположить произ­вольно. Пусть он будет направлен вдоль оси абсцисс. Вектор dA₁ рас­положим так, чтобы его начало совпало с концом вектора dA₀. Начало вектора dA₂ совместим с концом вектора dA₁ и т.д. После того как бу­дут построены таким образом все векторы dA_i, построим вектор суммы А, начало которого совпадает с началом вектора dA₀, а конец - с концом вектора dA_N. Угол между векторами dA_i и dA_i+1, равен разности фаз ∆φколебаний с номерами i и i + 1. Из (13.19) следует, что

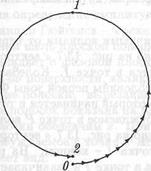
∆φ = к dR, т.е. каждый вектор повернут относительно предыдущего вектора на один и тот же угол. В таком случае, если бы все векторы dA_i имели одинаковую длину, они при их последовательном соединении образовали бы правиль­ный многоугольник, который в пределе при dR —>0 и N -> оо переходит

в окружность. Однако вследствие того, что длина dE_mi вектора dAi уменьшается при увеличении номера г, эти векторы при сложении обра­зуют ломаную линию, изображенную на рис. 13.5. В пределе при dR —> 0 и N —> оо эта линия превращается в спираль, которая "заканчивается" в точке С на рис. 13.6.

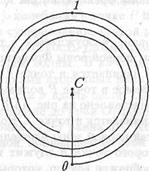
Рис. 13.5. Векторы, представля- Рис. 13.6. Векторы, представля­
ющие колебания, пришедшие от ющие колебания, пришедшие от
первых двух зон Френеля многих зон Френеля

Векторы dA_i ,которые расположены на рис. 13.6 в точках 0, 1, 2, ... образуют с осью абсцисс углы 0, π, 2π, ... Эти векторы представляют ко­лебания, возбуждаемые вторичными волнами, которые приходят в точку Р от границ зон Френеля. Таким образом, векторы dA_i , образующие дугу между точками 0 и 1, соответствуют колебаниям, возбуждаемым вторич­ными волнами от колец, лежащих внутри первой зоны Френеля; векторы dA_i, образующие дугу между точками 1 и 2, соответствуют колебаниям, возбуждаемым волнами от колец, лежащих внутри второй зоны Френеля, и т.д.

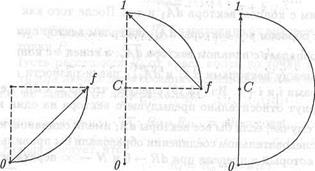
а) б) _б) г)

Рис. 13.7. Векторы, представляющие колебания, пришедшие: а) от первой половины первой зоны Френеля, б) от второй половины первой зоны Френеля, в) от первой зоны Френеля, г) от второй зоны Френеля

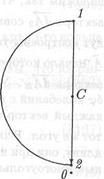
Колебание, возбуждаемое в точке Р вторичными волнами от первой половины первой зоны Френеля, представлено на рис. 13.7, а вектором, который начинается в точке 0 и заканчивается в точке f. Колебание, возбуждаемое в точке Р волнами от второй половины первой зоны Фре­неля, представлено на рис. 13.7, б вектором, который начинается в точке f и заканчивается в точке 1. Колебание, возбуждаемое в точке Р волна­ми от всей первой зоны Френеля, представлено на рис. 13.7, е вектором, для которого точка 0 служит началом, а точка 1 - концом. На рис. 13.7, г изображен вектор, который начинается в точке 1 и заканчивается в точке 2. Этот вектор представляет колебание, возбуждаемое в точке Р волнами от второй зоны Френеля. Колебание, возбуждаемое в точке Р вторичными волнами от всей волновой поверхности σ представлено на рис. 13.6 вектором, который начинается в точке 0 и заканчивается в точке С. Обозначим длину этого вектора Е_то. Величина Е_то есть ам­плитуда колебания, возбуждаемого в точке Р волнами от всей волновой поверхности. Иначе говоря, такой будет амплитуда колебаний в точке Р, когда экран с отверстием просто отсутствует. Из рис. 13.7, в видно, что амплитуда Е_т1 колебания, возбуждаемого в точке Р волнами от первой зоны Френеля, равна 2Е_т0.

Положение на векторной диаграмме вектора dA_N можно найти по зна­чению угла, который он образует с осью абсцисс. Этот угол равен разно­сти фаз ∆φ_N,0 между колебаниями, возбуждаемыми в точке Р волнами, приходящими из точки О и от краев отверстия. Согласно формуле (13.19)

∆φ_N,0 = k(R_N - R₀)

Соединив точку 0 на векторной диаграмме с. концом вектора с dA_N , полу­чим вектор суммы (13.21). Длина этого вектора, выраженная в долях от величины Е_то, есть искомая амплитуда Е_т колебания в точке Р.