Принцип Гюйгенса — Френеля. Совокупность явлений, наблюдаемых при распространении волн вбли­зи непрозрачных тел и в средах с неоднородной плотностью

Совокупность явлений, наблюдаемых при распространении волн вбли­зи непрозрачных тел и в средах с неоднородной плотностью, называется дифракцией. В частности, к этим явлениям относится огибание волнами препятствий и их проникновение в область геометрической тени.

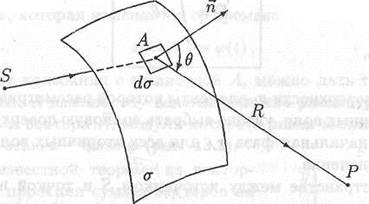
Рис. 13.1. К формулировке принципа Гюйгенса - Френеля

Теория дифракции основана на принципе Гюйгенса - Френеля. Со­гласно этому принципу, каждый элемент dσ поверхности σ, до которой дошла электромагнитная волна от некоторого источника S, можно рас­сматривать как источник вторичной электромагнитной волны (рис. 13.1). Колебания dE напряженности электрического поля, возбуждаемые вто­ричной волной от элемента dσ в произвольной точке Р за поверхностью σ, определяются формулой

dE=K(θ)(E_Adσ/R) cos(ωt - kR + a_A), (13.1)

где dE- одна из компонент вектора dE напряженности электрического поля во вторичной волне; ωиk- частота и волновое число; Еа и а_A -амплитуда и начальная фаза колебаний в некоторой точке А элемента поверхности da, которые вызваны волной, пришедшей от источника S;

R = АР - расстояние от элемента dσ поверхности σ до точки Р; dσ -площадь элемента поверхности. Выражение (13.1) отличается от сфе­рической волны только множителем К(θ), зависящим от угла θ между отрезком АР и нормалью к поверхности σ в точке А.

Множитель К(θ) принимает наибольшее значение при θ = 0, т.е. сре­ди вторичных волн, испускаемых элементом dσ, наибольшую амплитуду имеет волна, распространяющаяся в направлении нормали. При увели­чении угла θ множитель К(θ) убывает и обращается в ноль для θ = π/2.

Вторичные волны, испускаемые разными элементами dσ поверхности σ, когерентны. Колебание в точке Р согласно принципу суперпозиции есть результат интерференции вторичных волн:

E=∫_σdE (13.2)

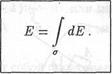
В качестве поверхности σ, элементы которой рассматриваются как ис­точники вторичных волн, удобно выбрать волновую поверхность, так как в этом случае начальная фаза а_а для всех вторичных волн будет иметь одно и то же значение.

Если в пространстве между источником S и точкой наблюдения Р имеются непрозрачные экраны, то поверхность σ следует выбрать таким образом, чтобы она совпадала с поверхностью экранов, а в отверстиях экранов имела форму волнового фронта первичной волны. При этом на поверхности непрозрачных экранов амплитуда колебаний источников вторичных волн принимается равной нулю, а на поверхности волнового фронта такой, какой она была бы при отсутствии экранов.

Решить при помощи формул (13.1) и (13.2) задачу о дифракции в об­щем случае очень трудно. Однако когда волна и преграда, на которую она падает, обладают каким-либо типом симметрии, найти распределе­ние интенсивности волн за преградой, хотя бы в некоторых точках про­странства, можно сравнительно легко.

В зависимости от условий наблюдения различают дифракцию Френе­ля и дифракцию Фраунгофера. Если источник света и точка наблюдения расположены от непрозрачной преграды настолько далеко, что волну, падающую на преграду, можно считать плоской, а лучи, идущие в точку Р, образуют практически параллельный пучок, то такой вид дифракции называют дифракцией Фраунгофера, или дифракцией в параллельных лучах. Дифракцию Фраунгофера можно наблюдать также в фокальной плоскости линзы. Если на экран с отверстием размера rпадает плоская с длиной волны λ, то характер дифракции определяется величи­ной

ξ=r²/(λl)

где l - расстояние от отверстия до точки наблюдения. При ξ<< 1 имеет место дифракция Фраунгофера. При ξ>> 1, т.е. для волн с достаточно короткой длиной волны, дифракция практически не наблюдается. Рас­пространение таких волн происходит по законам геометрической оптики. Дифракция волн, характеризуемая значениями параметра ξ ~ 1, назы­вается дифракцией Френеля.

13.2. Графический метод сложения гармонических колебаний f

Величине х, которая изменяется со временем по закону

х = A cos φ(t), (13.3)

т.е. совершает колебания с амлитудой А, можно дать геометрическую интерпретацию. А именно, эту величину можно рассматривать как про­екцию на ось х вектора А, модуль которого равен амплитуде А, а угол между ним и осью х - фазе φ (рис. 13.2).

Согласно известной теореме из вектор­ной алгебры, проекция суммы векторов на какое-либо направление равна сумме про­екций на это направление слагаемых векто­ров:

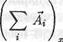=∑_iA_xi

Рис. 13.2. Вектор, представляющий гармоническое колебание

Поэтому для отыскания суммы функций

x=∑_ix_i = ∑_i А_icosφ_i(t)

можно поступить следующим образом. Каждое слагаемое в сумме (13.4) следует представить вектором A_i на плоскости, т.е. рассматривать i-е колебание как проекцию этого вектора на ось х:

A_i cos φ_i=(A_i)_x

Затем графически, например по правилу треугольника, следует найти

сумму

∑_iA_i =A

этих векторов (рис. 13.3). Вектор Абудет представлять суммарное ко­лебание (13.3). Амплитуда этого колебания равна модулю вектора А, а фаза φ- углу между вектором Аи осью х.

Фаза гармонического колебания φ = w t + а. Поэтому вектор, изобра­жающий такое колебание, будет вра­щаться с угловой скоростью ω. При сложении нескольких колебаний од­ной и той же частоты все векторы A_i, представляющие эти колебания, и вектор суммы А будут вращаться с одной скоростью. Так как при этом взаимное расположение векторов со

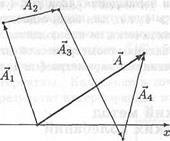
Рис. 13.3. Векторная диаграмма

временем не изменяется и модуль сум­марного вектора не зависит от време­ни, векторную диаграмму удобно строить для какого-либо произвольно­го момента времени, например, для момента t = 0. В этом случае углы, образуемые векторами A_i и А с осью х, будут равны начальным фазам а_i и а.