Дифракция света на круглом отверстии

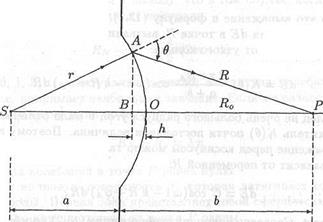
Монохроматический свет от точечного источника S падает на непро­зрачный экран с круглым отверстием. Источник расположен на оси сим­метрии отверстия на расстоянии а от экрана (рис. 13.4). При помощи принципа Гюйгенса - Френеля найдем амплитуду световых колебаний в точке Р на оси симметрии за экраном по другую сторону от источника света. Расстояние от экрана до точки Р равно b. В качестве поверхности, элементы которой будем рассматривать как источники вторичных волн, возьмем фазовую поверхность, "затягивающую" отверстие в экране. Для точечного источника такой поверхностью является сфера σ радиуса r, опирающаяся на края отверстия. Центр этой сферы находится там же, где источник. Сфера σ пересекается с осью SP в точке О на расстоянии R_o от точки Р. Очевидно, что

r + R₀ = a + b. (13.5)

Колебание dE, вызванное в точке Р вторичной волной от элемента dσ поверхности σ, расположенного около произвольной точки А, най­дем по формуле (13.1). Вследствие осевой симметрии выражение (13.1) не изменится, если элемент поверхности dσ перенести в другую точку А' поверхности σ, которая находится на том же расстоянии R от точки

Р, что и точка А. Поэтому вместо малого элемента поверхности мож­но взять узкое кольцо. При этом поверхностный интеграл (13.2) можно свести к определенному интегралу. Выберем в качестве переменной ин­тегрирования расстояние R и найдем выражение для площади dσ кольца, расстояние от внутреннего края которого до точки Р равно R, а рассто­яние до его внешнего края равно R + dR, где dR - произвольное малое приращение расстояния R.

Рис. 13.4- Дифракция света на круглом отверстии

Из элементарной геометрии известна формула для площади сфери­ческого сегмента σ= 2πrh, где h - высота сегмента, т.е. расстояние между точками В и О на рис. 13.4. При этом площадь узкого кольца будет

dσ = 2πrdh . (13.6)

Для того чтобы найти зависимость h от R, запишем теорему Пифагора для треугольников АВР и SAB:

R² = АВ² + (R₀ + h)² , r² = АВ² + (r – h)² .

Вычтем из первого равенства второе. После несложных вычислений с учетом (13.5) придем к зависимости

h = (R²- R₀)²/(2(a+b)) .

Дифференциал этой функции

dh = RdR/(a+b) .

При этом формула (13;6) принимает вид

dσ = 2πr RdR/(a+b) .

Подставив это выражение в формулу (13.1), получим следующее выра­жение для колебания dE в точке Р, вызванного вторичной волной, при­шедшей в эту точку от узкого кольца:

dE=K(θ)( 2πr E_A/(a+b)) cos(ωt - kR + a_A)dR (13.7)

Для колец не очень большого радиуса угол θ мало отличается от ну­
ля и множитель К(θ) почти постоянная величина. Поэтому в формуле
(13.7) выражение перед косинусом можно также считать величиной, которая не зависит от переменной R: ,

dE = C cos(ωt - kR + a_A)dR (13.8)

где С = const. Согласно принципу суперпозиции (13.2) колебание в точке Р будет выражаться определенным интегралом

E(t) = C cos(ωt - kR + a_A)dR , (13.9)

где R_n - расстояние от точки Р до края отверстия. Интегрирование по формуле Ньютона-Лейбница приводит к следующему результату:

Е= sin(ωt - kR + a_A)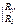

Преобразуем это выражение при помощи тригонометрической формулы

sin а- sin β = 2 sin((a-β)/2) cos ((a+β)/2) . (13.10)

Получим

E(t) = E_m cos( ωt-(1/2)k (R_o + R_N) + a _A) , (13.11)

где амплитуда колебания в точке Р

E_m = E_mo |sin(π (R_o + R_N)/λ)| (13.12)

E_mo = С/к.

Анализируя зависимость амплитуды колебания Е_т от рас­стояния R_n - R_o, приходим к выводу, что в том случае, когда разность R_n - Ro равна нечетному числу полуволн:

R_n - R_o = 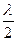(2n+1) , (13.13)

где п = 0, 1, 2, ... - натуральное число; амплитуда колебания Е_т = 2 Е_т0, т.е. принимает наибольшее значение. Если же разность R_n - R_o равна целому числу длин волн:

R_n - R_o =λn , (13.14)

то амплитуда колебаний в точке Р равна нулю.

Разделим волновую поверхность σ, которая затягивает отверстие в экране, на зоны. Первая зона представляет собой сферический сегмент, расстояния до краев которого от точки Р равны

R ⁽¹⁾ = R_o + λ/2

Вторая зона прилегает к первой и представляет собой кольцо, расстояние до

внутреннего края которого от точки Р равно R ⁽¹⁾ а до внешнего -

R ⁽²⁾ = R_o + λ .

Следующая зона есть кольцо, расстояния до краев которого от точки Р равны R ⁽²⁾ и

R ⁽³⁾ = R_o + (3/2)λ

и т.д. Эти зоны называют зонами Френеля. Если размеры отверстия в экране таковы, что волновая поверхность σ по отношению к задан­ной точке Р состоит из нечетного числа зон Френеля, то выполняется условие (13.13) и амплитуда световых колебаний в этой точке будет наи­большей. Если же волновая поверхность σ состоит из четного числа зон Френеля, то выполняется условие (13.14) и амплитуда колебаний в точке Р принимает наименьшее значение.