Интерференция света в тонких пленках. Рассмотрим интерференцию, возникающую при отражении света от двух поверхностей тонкого прозрачного слоя - интерференцию в тонких пленках

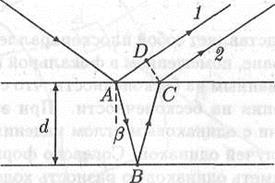
Рассмотрим интерференцию, возникающую при отражении света от двух поверхностей тонкого прозрачного слоя - интерференцию в тонких пленках. Пусть на пленку с показателем преломления п, находящуюся в вакууме, падает гармоническая световая волна. В результате отражения этой волны от верхней и нижней поверхностей пленки возникают две когерентные волны 1 и 2 (рис. 12.3).

Рис. 12.3. Образование когерентных волн при отражении лучей от

поверхности тонкой пленки

Согласно формулам (12.6) и (12.7) амплидуда и интенсивность све­товых колебаний в некоторой точке Р поля интерференции зависят от разности

φ₂-φ₁ фаз этих волн, которая в свою очередь, как это следует из формулы (12.18), определяется оптической разностью хода лучей ∆.

При расчете разности хода отраженных волн 1 и 2 необходимо учи­тывать следующее обстоятельство. Волна 1 образуется при отражении от среды с большим показателем преломления (оптически более плот­ной среды), тогда как волна 2 возникает при отражении от оптически менее плотной среды. Как показано в разделе 11.7, при отражении от оптически более плотной среды фаза колебаний светового вектора Е изменяется на π. При отражении от оптически менее плотной среды фаза светового вектора не изменяется. Таким образом возникает допол­нительная разность фаз отраженных волн, равная π. Это равносильно уменьшению (или увеличению) разности хода на величину λ/2. Поэтому

в рассматриваемом случае разность хода

∆ = п(АВ + ВС) - AD +λ/2 .

Используя законы отражения и преломления света, нетрудно получить формулу

∆ = 2ndcosβ + λ/2 (12.28)

где d - толщина пленки, β - угол преломления. Подстановка этого выра­жения в равенства (12.20) приводит к условиям максимумов и минимумов
при интерференции в тонкой пленке.

2nd cosβ = ((2m - 1) λ/2 для максимyма (12.29)

т λ для минимума,

где m = 1, 2, 3, ...

Пусть пленка представляет собой плоскопараллельный слой, а наблю­дение ведется на экране, помещенном в фокальной плоскости линзы, или глазом, аккомодированным на бесконечность, что соответствует положе­нию точки наблюдения на бесконечности. При этом в каждую точку экрана сходятся лучи с одинаковым углом падения на пленку, а значит cos β для всех этих лучей одинаков. Согласно формуле (12.28) все пары таких лучей будут иметь одинаковую разность хода, независимо от того, в какой точке они отразились от пленки. Наблюдаемая таким образом картина носит название полос равного наклона.

В случае пленки переменной толщины контрастную интерференцион­ную картину можно наблюдать с помощью линзы, проектирующей на экран поверхность пленки, или глазом, аккомодированным на пленку. Чтобы картина на экране была контрастной, необходимо, чтобы разность хода лучей, пришедших в одну точку экрана от разных точек протяжен­ного источника, была почти одинаковой. Этого можно достичь, исполь­зуя падение лучей на пленку, близкое к нормальному, и устанавливая перед линзой диафрагму. Тогда интервал изменения cosβ для лучей, интерферирующих в данном месте экрана, будет небольшим, и разность хода лучей будет почти одинаковой. На некотором небольшом участ­ке пленки cosβ также будет мало меняться, и результат интерференции будет определяться только толщиной пленки в месте падения на нее лу­ча. Каждая интерференционная полоса на экране будет соответствовать местам пленки с одинаковой толщиной. Такие полосы называются поло­сами равной толщины.

Задача. Используя законы отражения и преломления света, выве­сти формулу (12.28).