Когерентность

Амплитуда А и начальная фаза а гармонической волны

Е = A cos(wt - кх + а) (12.12)

не зависят от времени. Так как амплитуда суммы двух гармониче­ских колебаний, создаваемых гармоническими волнами в некоторой точ­ке пространства, определяется разностью а₂ - а₁ начальных фаз этих колебаний, она также не будет зависеть от времени.

В действительности идеальных гармонических волн не существует. Каждая реальная световая волна представляет собой совокупность волн, испущенных различными атомами. Поэтому амплитуда А и начальная фаза а являются беспорядочно изменяющимися функциями от времени и координат точки пространства. Характерное время изменения фазы t~10^-8с.

Глаза человека и различные оптические приборы регистрируют все­гда усредненную по некоторому интервалу времени Т интенсивность па­дающего на них света. Величина Т, называемая временем экспозиции, для разных оптических приборов может принимать различные значе­ния, но для всех приборов это время существенно больше времени τ. Два независимых источника света испускают волны, в которых хаотич­ные изменения фаз a₁(t, r) и a₂(t, г) происходят независимо друг от друга. Вследствие этого разность фаз φ₂ - φ₁ в формуле (12.7) также будет случайной функцией от времени. Поэтому при усреднении интер­ференционный член в формуле (12.7) обращается в ноль. В результате интенсивность света в каждой точке пространства будет равна сумме интенсивностей отдельных волн, т.е. интерференция наблюдаться не будет. О таких волнах говорят, что они некогерентны.

Для наблюдения интерференции света от двух реальных источников необходимо, чтобы разность фаз φ₂(t)-φ₁(t) в формулах (12.6) и (12.7) оставалась постоянной. Такие две волны называют когерентными. Для когерентных волн фазы φ₁ и φ₂ меняются не независимо друг от друга, а согласованно. С целью получения когерентных световых волн при­меняют различные способы разделения волны от одного источника на две части. Пройдя разные пути, эти две волны накладываются одна на другую в некоторой области пространства, которая называется полем интерференции,

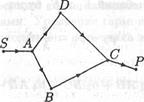
На рис. 12.1 от источника S в точку Р приходят две волны, одна из которых распространяется по "ломаному" лучу SABCP, а другая - по лучу SADCP. Пусть

Е_А = А_о cos(w t+a)

есть колебание, создаваемое электромагнитной волной в точке А. Най­дем колебания Е₁ и Е₂, которые вызваны в точке Р волнами, пришед­шими из точки А по различным путям.

Рис. 12.1. Схема образования когерентных волн

Скорость электромагнитной волны в среде меньше ее скорости в пу­стоте:

v=c/n (12.14)

здесь п - показатель преломления среды. Волновое число к связано с частотой ω и скоростью v соотношением

k=ω/v,

которое при помощи формулы (12.14) можно преобразовать к виду

k = пk₀, (12.15)

где

k₀=ω/c=2π/λ

к₀ и λ - волновое число и длина волны, распространяющейся в пустоте. Из формул (12.14) и (12.15) следует, что, когда электромагнитная волна пересекает границу раздела двух прозрачных сред с различными пока­зателями преломления, изменяется не только ее скорость, но и волновое число k.

Пусть свет проходит расстояние АВ, ВС и СР на рис. 12.1 в раз­личных средах, показатели преломления которых равны соответственно n₁, п₂ и n₃. В таком случае колебание, вызванное в точке Р волной, пришедшей из точки А вдоль луча АВСР, будет иметь вид

Е₁ = А₁ cos (ωt- к₀ (n₁ АВ + п₂ ВС + п₃ СР) + а₀)(12.16)

Аналогично можно записать формулу для колебания, вызванного в точке Р волной, пришедшей из точки А вдоль луча ADCP:

Е₂ = А₂ cos (ω t - к₀ (n₄ AD + п₅ DC + n₃ СР) + a₀) , (12.17)

где n₄ и n₅ - показатели преломления сред, в которых лежат лучи AD и DC. Разность фаз колебаний Е₁ и Е₂ будет

φ₂-φ₁ = (π/λ)∆ , (12.18)

где величина

∆ = n₁ АВ + п₂ ВС - n₄ AD - п₅ DC

называется оптической разностью хода лучей. Как видно, эта величина имеет размерность длины и отличается от геометрической разности хода АВ + ВС - AD - DC тем, что длина каждого отрезка луча умножается на показатель п преломления среды, в которой распространяется свет.

Используя формулу (12.18), условия максимума (12.8) и минимума (12.10) можно записать следующим образом:

для максимума, для минимума.

m λ для максимума

∆ = (12.20)

(2m+1) λ для минимума

Согласно этим условиям при интерференции двух волн в некоторой точ­ке Р по схеме на рис. 12.1 в этой точке будет наблюдаться максимум интенсивности света, когда оптическая разность хода двух лучей равна

целому числу длин волн. Если же оптическая разность хода лучей рав­на нечетному числу полуволн, то в точке Р будет наблюдаться минимум интенсивности света.

Устройства, в которых осуществляется разделение волны для получе­ния интерференции, называются интерференционными схемами. К ним относятся схема Юнга, бипризма Френеля, зеркало Ллойда и др. При использовании в интерференционных схемах обычного (не лазерного) ис­точника света интерференция наблюдается только при сравнительно ма­лой оптической разности хода двух частей волны. Если разность времен, затрачиваемая двумя половинами волны на распространение от источ­ника до места встречи, превышает характерное время г изменения фазы источника, две половины волны становятся некогерентными между со­бой, и интерференция не наблюдается.

Подводя итоги, отметим, что для наблюдения интерференционной картины необходимо выполнение следующих условий: складывающие­ся волны должны иметь одинаковую частоту и одинаковое направление колебаний, амплитуды их не должны сильно отличаться одна от другой, волны должны быть когерентными.

,