Интерференция света. Когерентность и монохроматичность световых волн. Оптическая длина пути и оптическая разность хода лучей.

При наложении световые волн выполняется принцип суперпозиции: результирующий световой вектор является суммой световых векторов отдельных волн. При этом может получиться волна, интенсивность которой не будет равна сумме интенсивностей складывающихся волн.

Интерференция свойственна не только световым волнам, являющимися по своей природе электромагнитными волнами, но и волнам любого другого типа. Поскольку волны любого вида удовлетворяют одним и тем же волновым уравнениям, то при описании интерференции любых видов волн применяется один и тот же математический аппарат. Поэтому, сущность интерференции рассмотрим на примере сложения двух одномерных гармонических волн (волн вида 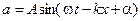) одинаковой частоты. Накладываясь друг на друга, они возбуждают в некоторой точке пространства гармонические колебания

,

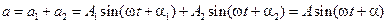амплитуда которых определяется выражением

.
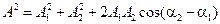Интенсивность волны пропорциональна квадрату амплитуды 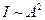. Поэтому, наблюдаемая при наложении волн интенсивность

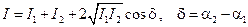. (17-1)
Результат сложения зависит от разности фаз d (меняющейся при переходе к другой пространственной точке). В тех точках пространства, для которых 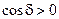, 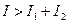; в точках, для которых , .

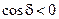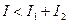Таким образом, при наложении гармонических (в общем случае когерентных) световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн.

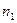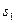Рассмотрим точечный источник света S, который излучает монохроматический свет (свет фиксированной частоты) (рис.17.1). До точки P первый луч проходит в среде с показателем преломления путь , второй луч проходит в среде с показателем преломления 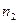путь 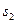. Если в точке S фаза колебаний равна 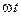, то первый луч возбудит в точке P колебание 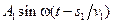, а второй луч – колебание 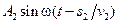( 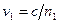и 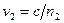– фазовые скорости волн). Следовательно, разность фаз колебаний, возбуждаемых лучами в точке P, будет равна

.

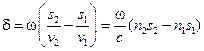Множитель 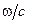равен 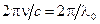( 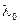– длина волны в вакууме) и выражению для разности фаз можно придать вид

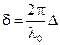, (17-2)

где 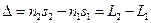(17-3)

есть величина, называемая оптической разностью хода.

Из формулы (17-2) видно, что если оптическая разность хода равна целому числу длин волн в вакууме

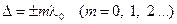, (17-4)

то разность фаз 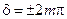и колебания будут происходить с одинаковой фазой. Следовательно, условие (17-4) есть условие интерференционного максимума.

Если D равна полуцелому числу длин волн в вакууме,

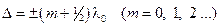, (17-5)

то 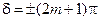, так что колебания в точке P находятся в противофазе. Условие (17-5) есть условие интерференционного минимума.

В реальности монохроматических волн (неограниченных во времени волн фиксированной частоты) не существует. Для реальных световых волн необходимым условием интерференции является их когерентность. Так называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

Некогерентность естественных источников света обусловлена тем, что излучение светящегося тела складывается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью ~10^-8 с и протяженностью около 3 м независимо друг от друга. Начальные фазы этих волновых цугов никак не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы цугов при следующих актах излучения меняются случайным образом.

Расчет интерференционной картины от двух источников. Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников 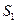и 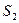, имеющих вид параллельных, тонких светящихся нитей либо узких щелей (рис.17.2). Если в области, в которой волны перекрываются, внести экран, то на нем будет видна интерференционная картина, которая имеет вид чередующихся светлых и темных полос. Рассчитаем положение полос и их ширину. Экран

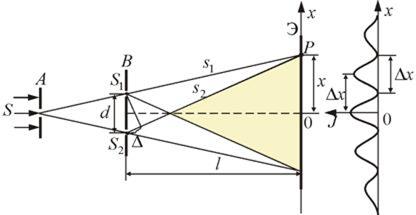
Рис.17.2

поместим параллельно обеим щелям на одинаковом расстоянии l. Начало отсчета выберем в точке O, относительно которо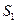й и 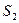расположены симметрично. Источники будем считать испускающими свет в одинаковой фазе. Из рисунка видно, что

, .

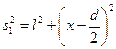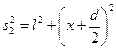Следовательно,

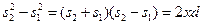
оптическая разность хода равна

.

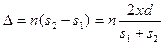Разность хода 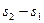составляет несколько длин волн и всегда значительно меньше 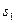и 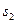( 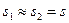). Поэтому можно положить 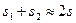и

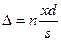. (17-6)

В большинстве случаев l>>d, поэтому 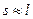, т.е.

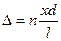(17-7)

Подстановка значения D в условие (17-4) дает, что максимумы интенсивности будут наблюдаться при значениях

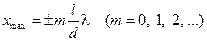. (17-8)

Здесь 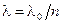– длина волны в среде.

Подставив (17-7) в условие (17-5), получим координаты минимумов интенсивности

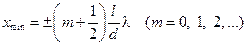. (17-9)

Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами –шириной интерференционной полосы. Из (17-8) и (17-9) следует, что эти расстояния имеют одинаковое значение

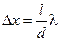. (17-10)